Homework 3: Complex Arithmetic

This homework is due on Wednesday, April 12, at 11:59:59 PM (Eastern daylight time). You must use submit to turn in your homework like so:
submit cs411_jtang hw3 hw3.c hw3.circ
The grader will use the supplied Makefile to compile your work. In addition, each submitted source code file must have a file header comment, as described on the coding conventions page. For the Logisim file, place your name and assignment number in a text label on the main circuit.

You can only complete this assignment within an ARMv8-A development environment, and thus you must have completed the first homework before attempting this assignment. In addition, you must have a working 16-bit ALU from the first project.

Back in the old days, computers were built to perform only integer arithmetic, as that the CPU lacked support for floating point calculations. For example, the original Intel systems deferred floating point to an optional coprocessor, the Intel 8087 chip. Furthermore, integer multiplication and integer division were implemented by the coprocessor, not the main CPU. For users that did not have an Intel 8087, they relied upon specialized libraries to implement floating point and advanced arithmetic operations purely in software. These became known as soft floating point systems.

In this assignment, you will build a portion of a mathematical library. You will write code, in C, to parse bitwise representation of floating point numbers. You will then implement floating point multiplication. Finally, you will add more logic components to your Logisim file to support the second project.

Part 1: Floating Point Parser

To begin, create a directory for your assignment and download the following files into that directory via wget:

http://www.csee.umbc.edu/~jtang/cs411.s23/homework/hw3/hw3.c: Skeleton code for this assignment.
http://www.csee.umbc.edu/~jtang/cs411.s23/homework/hw3/Makefile: Builds the code for this assignment, by simply running make. Also included is a clean target to remove all built objects. You do not need to modify this file, nor should you submit it with your work.

Furthermore, copy your proj1.circ file from the first project, and rename that copy as hw3.circ. You will modify hw3.circ in Part 4. Note, you do not need to write any assembly code for this homework.

Now run make to compile everything. The program takes two integer parameters. The given skeleton code converts those parameters into two 16-bit values.

Your first job is to implement half_float_parse(). This function interprets its 16-bit incoming parameter val as an IEEE-753 half floating point value. That is, given val, display the sign bit, exponent, and significand bits. Then show what kind of floating point value val is, which is one of:

Normal
Negative Zero
Denormalized
Infinity, both positive and negative
Not a Number, both positive and negative

In your output, show the sign bit. Then show the decimal form of the exponent and its actual magnitude (as a decimal, and without its bias of 15 for normal values). Then display the bits associated with the significand, as a hexadecimal value, including the implied one (for normal) or zero (for denormal) bit. Finally, if the bits within val represent a special value, then state it as such. The function returns true if the value is normal, false otherwise.

As an aid to your parsing, the given C code displays val as if it were a float. Be careful with your shifting and bit masks. Be aware of what C's ">>" really does, and use correct variable types to hold intermediary values.

Part 2: Unsigned Integer Multiplication

The next task is to implement uint16_mult(). Read the function comments in hw3.c. Implement a constant-time multiplication algorithm of your choice. Note that you are performing 16-bit unsigned integer multiplication; therefore the product will be 32-bits. See the Extra Credit option described below for a more challenging implementation.

Restriction 1: Your implementation must execute in constant time, regardless of input parameters. You may not simply iterate i1 times, adding i2 to the product for each iteration.

Restriction 2: You may not use the built-in multiplication, division, nor modulo division instructions for this assignment. That would be cheating, wouldn't it? You are limited to only adds, subtracts, shifts, rotates, bitmasks, bitwise logic, compares, and branches.

In the next assignment, you will translate your Part 2 code into assembly. It is in your best interest to write the code cleanly, with plenty of comments.

Part 3: Floating Point Multiplication

Next, implement half_float_mult(), as per its function comments. This function takes as input two normal half-floating point value. You are to calculate their half-floating point product. You may assume the resulting value will also be a normal half-floating point values.

Restriction 3: Like with Part 2, your code may not use real multiplication. Instead, you must use your uint16_mult() function to calculate the significand.

The sign bit and exponent bits are easy to calculate. Determining the significand bits is harder. Don't forget to add the implied leading 1 to the 10-bit significands, when calling uint16_mult(). Because you are multiplying two 11-bit values, the result is a 22-bit value: 2 bits to the left of the decimal point, and 20 bits to the right. You need to re-normalize this value like so:

If bit 21 is a 1, then shift everything to the right and increment the exponent.
Otherwise as long as bit 20 is a 0, shift everything to the left and decrement the exponent.

Then store the first 10 bits to the right of the decimal point in your result, along with the sign bit and exponent bits. You are not required to round the value to the nearest even. (The grading criteria is lenient; it allows your code's LSB to be off by one from the real result.)

Part 4: Logic Components

In the first project you created a 16-bit ALU. Prepare your hw3.circ for the final project by removing the Roulette subcircuits: Roulette, Roulette SM, Roulette Player, and Roulette Ball. Keep your ALU subcircuits. Then create a new subcircuit called Main. Move Main to be the top-most circuit.

Create a new subcircuit, Register File. This register file must hold eight 16-bit registers. It has these seven inputs:

ASel (3 bits): Selects a register to route out through the A Bus.
BSel (3 bits): Selects a register to route out through the B Bus.
WSel (3 bits): Selects a register to route out through the W Bus, and also which register to update.
WEn (1 bit): If true and Clk is true, then update the register specified by WSel.
WData (16 bits): Value to store into the register file, when WEn and Clk are true.
0 (1 bit): Reset line. If true, unconditionally reset all register values to zero.
Clk (1 bit): If true and WEn is true, then update the register specified by WSel using the value at WData.

The register has three outputs, A Bus, B Bus, and W Bus. These are all 16-bits, and their values are selected by ASel, BSel, and WSel, respectively.

Caution: The register file is only to be updated when both WEn and Clk are true. Many previous students connected Clk to both the register's enable and clock ports. This is incorrect. Clk only connects registers' clock ports.

Your system will have a 16-bit Program Counter register that is incremented by 1 after most clock cycles. Create another subcircuit, PC Control Unit, based upon the Instruction Fetch Unit from Lecture 12. This subcircuit has these inputs:

CurPC (16 bits): Current Program Counter value.
Imm (16 bits): Alternative program address.
PCSel (1 bit): If false, select CurPC, incremented by 1. Otherwise, select Imm.

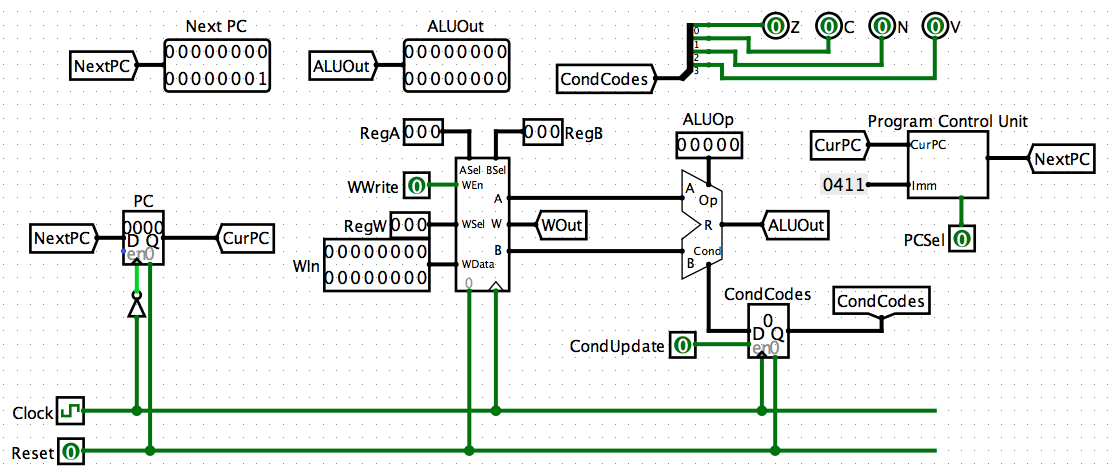
In your Main, add a Program Counter, Register File, 16-bit ALU, and PC Control Unit. Store the condition codes in a 4-bit register, with its own enable control. Add a splitter to that register's output, to easily monitor their values. Note the use of tunnels to make the subcircuit more understandable.

For now, add a dummy constant input to PC Control Unit. Test that your PC increments by repeatedly poking the clock line and changing PCSel. Ensure the PC is updated on a falling edge.

The connections between your register file, ALU, PC control unit, and clock line will be modified further in the next assignment.

Part 5: Required Documentation

Add a comment block to the top of hw3.c file that answers the following scenario. In Part 3, you had to normalize the significand such that it has a leading 1 to the left of the decimal point. Suppose you were to build a hardware circuit to perform this operation, where the curcuit has these two inputs:

Exponent (5 bit): Half-float exponent, before normalizing
Significand (22 bit): 22-bit product, before normalizing

How can the circuit calculate the normalized values for both Exponent and Significand within a single clock cycle? Assume the result can be normalized.

Sample Output

Here is a sample output from running the program. The grader will use different values to test your submission.

$ ./hw3 0x441c 0x4436
For the bit pattern 0x441c (half float value: 4.10938):
  Sign bit: 0
  Significand: 0x41c
  Exponent bits: 17 (actual magnitude: 2)
    normal
For the bit pattern 0x4436 (half float value: 4.21094):
  Sign bit: 0
  Significand: 0x436
  Exponent bits: 17 (actual magnitude: 2)
    normal
Part 2: unsigned integer multiply 0x441C and 0x4436:
  correct result: 0X1225CDE8
  your result:    0X1225CDE8
Part 3: half-float multiply 4.10938 and 4.21094:
  correct result: 0x4C53
  your result:    0x4C53

$ ./hw3 0xabcd 0x6543
For the bit pattern 0xabcd (half float value: -0.0609436):
  Sign bit: 1
  Significand: 0x7cd
  Exponent bits: 10 (actual magnitude: -5)
    normal
For the bit pattern 0x6543 (half float value: 1347):
  Sign bit: 0
  Significand: 0x543
  Exponent bits: 25 (actual magnitude: 10)
    normal
Part 2: unsigned integer multiply 0xABCD and 0x6543:
  correct result: 0X43F4D7A7
  your result:    0X43F4D7A7
Part 3: half-float multiply -0.0609436 and 1347:
  correct result: 0xD521
  your result:    0xD521

$ ./hw3 0xfc00 0x0300
For the bit pattern 0xfc00 (half float value: -inf):
  Sign bit: 1
  Significand: 0x000
  Exponent bits: 31 (actual magnitude: -14)
    * negative infinity
For the bit pattern 0x0300 (half float value: 4.57764e-05):
  Sign bit: 0
  Significand: 0x300
  Exponent bits: 0 (actual magnitude: -14)
    * denormalized
Part 2: unsigned integer multiply 0xFC00 and 0x0300:
  correct result: 0X2F40000
  your result:    0X2F40000

Other Hints and Notes

Ask plenty of questions on the Blackboard discussion board.
At the top of your submitted files, list any help you received as well as web pages you consulted. Please do not use any URL shorteners, such as goo.gl or TinyURL. Also, do not cite shared data services, such as Pastebin, Dropbox, or Google Drive.
C99 introduced fixed-width integer types. This assignment intentionally uses them, to force the compiler to use certain register assignments.
During lecture the Program Counter was always incremented by 4, but for this homework increment it instead by 1. This is due to a limitation of Logisim, and will be further explained in the next assignment.

Extra Credit

You may earn an additional 10% credit for this assignment by implementing a more difficult form for uint16_mult(), by implementing Booth's algorithm. As before, you may not use multiplication, division, nor modulo division instructions. You may assume that both operands will be unsigned integer values.

If you choose to perform this extra credit, put a comment at the top of your hw3.c file, alerting the grader.

CMSC 411:

Computer Architecture