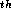element of an array of linked lists; each linked list will represent
one bucket. Here we assume that there are 137 buckets (we will
therefore want to pick a different hash function than the one
presented above):
CMSC--202 Computer Science II for Majors
Fall 1997 5 November 1997 Search
In the language of computer science, searching is the process of examining a set of data records to find one record that has particular characteristics. Often, we will know one field of a data record ( e.g., a Social Security number) and we are interested in finding the record that contains that known value. The portion of data that is known is called the key. When we search, we might be interested in finding other data associated with the key ( e.g., the person's name), or in determining whether the key is present in the data, or in finding the place in the storage structure that holds the key.
This handout presents three search methods: linear search, binary search, and hashing. Each of the search routines presented takes three types of arguments: a set of data through which to search; a key item for which we are searching; and a comparator for comparing a data item against the key. Two definitions are needed throughout the code in this handout. First, FAIL is defined as a legal return value that is distinguishable from items in the search set. For example, if the items to be stored are strings, then NULL might be a reasonable choice for FAIL:
#define FAIL NULL
Second, the comparator needs a way to indicate how its two arguments
are related. We will use an enum to express three possible
relationships: the key precedes the given data item according to
some ordering of the data ( e.g., the key is 42, the item is
17, and we are using reverse numerical order); the key
matches the item ( e.g., the key is 'Q', the item is 'Q',
and we are using ASCII order); or the key comes after the
item ( e.g., the key is "foo", the item is "bar",
and we are using alphabetic order):
typedef enum {
precedes,
equal_to,
follows
} comparison_result;
In Linear Search, we search for an item that matches the key by examining every item in the search set one item at a time. Here is an implementation of linear search in a linked list:
list_item_type
linear_search(list_type list,
key_type key,
comparison_result (*comparator)(key_type, list_item_type))
{
if (empty_list(list))
return(FAIL);
else if (comparator(key, first(list)) == equal_to)
return(first(list));
else return(linear_search(rest(list), key, comparator));
}
Here is an implementation of linear search in an array. Notice that the set of elements to be searched is conveyed through two arguments: an array, and a count of the number of elements in that array:
#define ARRAY_MAX 128
typedef int array_item_type; /* or whatever */
typedef array_item_type array_type[ARRAY_MAX];
array_item_type
linear_search_array(array_type arr,
int arr_size,
key_type key,
comparison_result (*comparator)(key_type, array_item_type))
{
int i;
for (i = 0; i < arr_size; i++)
if (comparator(key, arr[i]) == equal_to)
return(arr[i]);
return(FAIL);
}
Linear search is a brute--force method; it does not exploit any knowledge we might have about the organization of our data. If we know something about that organization, it is sometimes possible to reduce the amount of work we need to do to find a desired item. Binary search is one such method. In binary search, we assume that the data to be searched are stored in a binary tree such that each left descendant of a node precedes that node, while each right descendant of a node follows that node. Such a tree is called an ordered binary tree. By comparing the key to the item at the root of an ordered binary tree, we can immediately determine whether the desired item resides in the left subtree or the right subtree. Here is an implementation of binary search in an ordered binary tree:
tree_item_type
binary_search(tree_type tree,
key_type key,
comparison_result (*comparator)(key_type, tree_item_type))
{
if (empty_tree(tree))
return(FAIL);
else switch(comparator(key, tree_data(tree))) {
case precedes:
return(binary_search(left_child(tree), key, comparator));
break; /* Just as a safety habit */
case equal_to:
return(tree_data(tree));
break;
case follows:
return(binary_search(right_child(tree), key, comparator));
break;
}
}
We can view an ordered array as if it were a binary tree by imagining that the middle array element is the root, the values to its left make up its left subtree, and the values to its right make up its right subtree. Here is an implementation of binary search in an ordered array. Note that the set of data items to be searched is now conveyed through three parameters: an array, and lower and upper bounds within the array:
array_item_type
binary_search_array(array_type arr,
int low,
int high,
key_type key,
comparison_result (*comparator)(key_type, array_item_type))
{
int mid;
if (low > high)
return(FAIL);
else {
mid = (low + high) / 2;
switch(comparator(key, arr[mid])) {
case precedes:
return(binary_search_array(arr, low, mid-1, key, comparator));
break;
case equal_to:
return(arr[mid]);
break;
case follows:
return(binary_search_array(arr, mid+1, high, key, comparator));
break;
}
}
}
Hashing is a search method in which each item to be searched for is assigned to one of a set of `buckets.' When an item is sought, only the single bucket to which it would be assigned is examined. If there are many buckets and the items are distributed evenly across the buckets, then each bucket will have relatively few items (making for a rapid search).
A hash function is a function that determines to which bucket a given item should be assigned. Here is an example of a hash function for strings. This function assumes that the string being hashed begins with a capital letter. The hash function assigns the string to one of twenty--six buckets according to the first letter of the string (strings that begin with `A' are assigned to bucket zero, strings that begin with `B' are assigned to bucket one, etc.):
int
hash(hash_item_type item)
{
assert(item != NULL);
assert(isupper(item[0]));
return(item[0] - 'A');
}
In our implementation, a hash table will be a pointer to the zero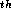
element of an array of linked lists; each linked list will represent
one bucket. Here we assume that there are 137 buckets (we will
therefore want to pick a different hash function than the one
presented above):
#define NUM_BUCKETS 137 typedef char *hash_item_type; typedef hash_item_type list_item_type; #include "lists.h" typedef list_type *hash_table_type;
The function create_hash_table creates a new hash table and initializes each of its buckets to be empty. Calloc is like malloc, except that it allocates enough space to hold many items of the given size; the number of items is specified by calloc's first argument, while the size of each item is specified by its second argument:
hash_table_type
create_hash_table(void)
{
int i;
hash_table_type result;
result = calloc(NUM_BUCKETS, sizeof(list_type));
assert(result != NULL);
for (i = 0; i < NUM_BUCKETS; i++)
result[i] = the_empty_list;
return(result);
}
To retrieve an item from a hash table, we will first use our hash function
to determine which bucket to search, then use linear search (as given
in Section 1) to look
through each of the items in that bucket. For simplicity, we will
assume that the key is an entire hash_item_type:
hash_item_type
get_hash(hash_table_type hash_table,
hash_item_type item,
comparison_result (*comparator)(hash_item_type, hash_item_type))
{
return(linear_search(hash_table[hash(item)], item, comparator));
}
At most one copy of each item will be placed in a bucket. Therefore, enter_hash, the routine that adds an item to a hash table, must first call get_hash to determine whether the item is already there:
void
enter_hash(hash_item_type item,
hash_table_type hash_table,
comparison_result (*comparator)(hash_item_type, hash_item_type))
{
if (get_hash(hash_table, item, comparator) == FAIL) {
int hash_value;
hash_value = hash(item);
hash_table[hash_value] = cons(item, hash_table[hash_value]);
}
}
The hash function given on Page 
does not do
a very good job of
distributing strings evenly across the buckets. For example,
if we are hashing English words, then the bucket containing words that
start with `S' will be quite full, while the bucket containing words
that start with `X' will be almost empty. A better hash function will
assign strings more evenly across the buckets:
int
hash(hash_item_type item)
{
int result;
char *ptr;
result = 0;
for (ptr = item; *ptr != '\0'; ptr++)
result = (result * 5179 + *ptr) % NUM_BUCKETS;
return(result);
}
Notice that this hash function takes every letter of the string into consideration when choosing a hash bucket. Here is a recursive implementation of essentially the same hash function:
int
hash(hash_item_type item)
{
if (item[0] == '\0')
return(0);
else return((hash(item + 1) * 5179 + item[0]) % NUM_BUCKETS);
}