CMSC--202 , Section Computer Science II for Majors
Fall 1997 9 October 1997 Homework 4
Assigned: 7 Oct
Due Date: 16 Oct
Late Date: 18 Oct
One of the advantages to having function pointers in C is that they
allow us to construct strong abstraction barriers. We saw, as an
example, that we could separate the functionality of plotting a
function from actually knowing the function we intend to plot. In
this way, the generality of our plotting function is extended - our
solution could be applied to plot any function.
We would like to develop an abstraction for computing the root of an equation of the
form 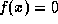 . For example, if
. For example, if
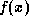 is
is 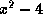 , a root of the equation
, a root of the equation
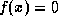 is found when x is 2 (or -2). When
is found when x is 2 (or -2). When 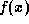 and its
derivative,
and its
derivative, 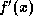 are both continuous and
are both continuous and 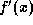 is not equal to
0, we can apply the Newton-Raphson method to find a root of f.
The method is given by this algorithm:
is not equal to
0, we can apply the Newton-Raphson method to find a root of f.
The method is given by this algorithm:
- Make an initial guess
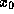 for a root of the equation. If
for a root of the equation. If 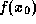 equals 0, then we have found a root of the equation, and we are done -
just return
equals 0, then we have found a root of the equation, and we are done -
just return 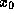 . (Note that if
. (Note that if 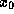 is not a root of f,
then we must make sure that
is not a root of f,
then we must make sure that 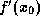 is not 0 -- make a new guess.)
is not 0 -- make a new guess.)
- If
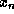 is not a root
( i.e.,
is not a root
( i.e., 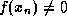 ), compute
), compute
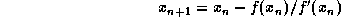
This value is guaranteed to be closer to the root of the equation than
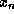 .
.
- If
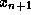 is a root, return it. Otherwise, go to
step 2.
is a root, return it. Otherwise, go to
step 2.
Example: Suppose that we want to solve the equation
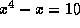 . This is equivalent to solving
. This is equivalent to solving 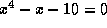 .
The derivative of this function is
.
The derivative of this function is
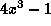 .
Suppose we guess
.
Suppose we guess 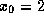 . Then
. Then
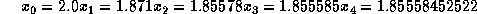
It can be shown that the difference between 1.85558452522 and an actual root of f is
less than 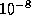 .
.
You will need to code a function to implement the Newton-Raphson
method for finding a root of an equation. Given the following type
definition:
typedef void * (*functype)(double *)
The prototype for newton would be:
double newton (functype fn, functype deriv, double epsilon);
Declarations and explanation of functions of type functype are
given in sample interface file funs.h on page  .
You will write the function newton and any auxiliary functions
you decide are necessary, to implement the Newton-Raphson method for
finding a root of an equation. You will also write an implementation
file for funs.h.
Test your code with the driver in the file hw4.c given on
page
.
You will write the function newton and any auxiliary functions
you decide are necessary, to implement the Newton-Raphson method for
finding a root of an equation. You will also write an implementation
file for funs.h.
Test your code with the driver in the file hw4.c given on
page  .
You must also provide a makefile, named either makefile or
Makefile. Your makefile must produce an executable named hw4.
.
You must also provide a makefile, named either makefile or
Makefile. Your makefile must produce an executable named hw4.
You may recall from your 201 days that a floating point number is an
approximation to a decimal number. It almost always is impossible to
test for equality between two values of type float or double, and if
we (naively) try to use the expression
if (f(z) == 0)
as a test for terminating our algorithm, we will most likely find
ourselves in trouble, because f(x) will almost certainly
never be exactly zero. What's a poor programmer supposed to do,
anyway? We will test for something we'll call approximate equality.
Suppose that epsilon is some small quantity, say 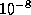 .
Then we say that 2 values,
.
Then we say that 2 values, 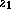 and
and  , of type double, are
approximately equal when
, of type double, are
approximately equal when 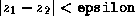 . The
expression |Z| is the absolute value of Z. The function
fabs, found in math.h, returns the absolute value of its argument.
Note that the call to newton passes a parameter, epsilon. In
the example driver, epsilon is set to
. The
expression |Z| is the absolute value of Z. The function
fabs, found in math.h, returns the absolute value of its argument.
Note that the call to newton passes a parameter, epsilon. In
the example driver, epsilon is set to 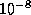 .
.
Submit all files needed to make the executable hw4, including header
file(s), implementation file(s), and your makefile.
To submit your files, do
submit cs202_01 hw4 file1 file2 . . .
replacing "file1 file2 . . ." with your files. You don't need to
submit a typescript file for this project. We will compile and run
your code using your submitted makefile.
Remember that if you use functions from the math library, you must use
the -lm flag on the appropriate cc lines of your makefile.
Here is the output produced by the sample driver on
page  . The interface for the functions tested is
given on page
. The interface for the functions tested is
given on page  .
.
Driver for Newton-Raphson function
A root of [x ^ 4 - x - 10 = 0] is 1.855585. f(1.855585) = 0.000000
A root of [sin(1 + x) - 2 * x = 0] is 0.498701. f(0.498701) = -0.000000
Please read the sample interface on page  carefully. Notice that each function is ``self-aware.''
What it returns is controlled by its parameter value. If
passed NULL, it returns a string that describes the
function. If passed a non- NULL value, it computes the value
represented by the function.
carefully. Notice that each function is ``self-aware.''
What it returns is controlled by its parameter value. If
passed NULL, it returns a string that describes the
function. If passed a non- NULL value, it computes the value
represented by the function.
/*
funs.h
Interface for functions for HW-4 CMSC-202 Fall 1997
Thomas Anastasio
Created: 3 October 1997
Current: 3 October 1997
*/
/* Note:
* Each function is either a function or its first derivative. In each
* case, the function returns a descriptive string if the argument x is
* NULL. Otherwise it returns a pointer to a double which is the value
* of the function taken at the value pointed to by x.
* Example: Suppose fun1 computes the square of the double pointed to
* by its argument. Suppose y is declared as double y = 3.0;
* Then,
* fun1(NULL) returns a char pointer that points to
* the string "x ^ 2"
* and
* fun1(&y) returns a double pointer that points to
* a double having value 9.0
*/
#ifndef FUNS_H
#define FUNS_H
/* In all of the following comments, X means the double
* pointed to by the argument x.
*/
/* fun1
* X ^ 4 - X - 10
*/
extern void * fun1(double * x);
/* fun1prime
* 4 * X ^ 3 - 1 (derivative of fun1)
*/
extern void * fun1prime(double * x);
/* fun2
* sin(1 + X) - 2 * X
*/
extern void * fun2(double * x);
/* fun2prime
* cos(1 + X) - 2 (derivative of fun2)
*/
extern void * fun2prime(double * x);
#endif
/*
hw4.c
Main function for HW-4 CMSC-202 Fall 1997
Thomas Anastasio
Created: 3 October 1997
Current: 3 October 1997
*/
#include <stdio.h>
#include <stdlib.h>
#include "newton.h"
#include "funs.h"
#ifndef EPSILON
#define EPSILON 1.0e-8
#endif
typedef functype flist_type[2];
main()
{
flist_type funcs = {fun1, fun2};
flist_type derivatives = {fun1prime, fun2prime};
int i;
int nfuncs; /* number of functions to test */
double root; /* root of the function */
double fz; /* value of the function at the root */
printf("\n\nDriver for Newton-Raphson function\n");
nfuncs = sizeof(funcs)/sizeof(functype);
for (i = 0; i < nfuncs; ++i)
{
root = newton(funcs[i], derivatives[i], EPSILON);
fz = *(double *)(funcs[i])(&root);
printf("\n A root of [%s = 0] is %lf. f(%lf) = %lf\n",
(char *)(funcs[i])(NULL), root,root,fz);
}
}
Thomas A. Anastasio
Thu Oct 9 10:53:05 EDT 1997
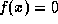 . For example, if
. For example, if
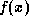 is
is 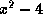 , a root of the equation
, a root of the equation
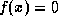 is found when x is 2 (or -2). When
is found when x is 2 (or -2). When 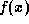 and its
derivative,
and its
derivative, 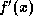 are both continuous and
are both continuous and 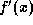 is not equal to
0, we can apply the Newton-Raphson method to find a root of f.
The method is given by this algorithm:
is not equal to
0, we can apply the Newton-Raphson method to find a root of f.
The method is given by this algorithm:
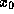 for a root of the equation. If
for a root of the equation. If 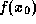 equals 0, then we have found a root of the equation, and we are done -
just return
equals 0, then we have found a root of the equation, and we are done -
just return 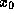 . (Note that if
. (Note that if 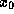 is not a root of f,
then we must make sure that
is not a root of f,
then we must make sure that 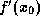 is not 0 -- make a new guess.)
is not 0 -- make a new guess.)
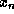 is not a root
( i.e.,
is not a root
( i.e., 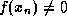 ), compute
), compute
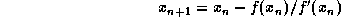
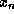 .
.
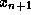 is a root, return it. Otherwise, go to
step
is a root, return it. Otherwise, go to
step 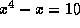 . This is equivalent to solving
. This is equivalent to solving 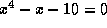 .
The derivative of this function is
.
The derivative of this function is
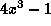 .
Suppose we guess
.
Suppose we guess 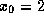 . Then
. Then
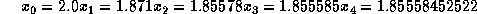
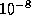 .
.

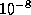 .
Then we say that 2 values,
.
Then we say that 2 values, 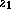 and
and  , of type double, are
approximately equal when
, of type double, are
approximately equal when 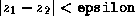 . The
expression |Z| is the absolute value of Z. The function
fabs, found in math.h, returns the absolute value of its argument.
Note that the call to newton passes a parameter, epsilon. In
the example driver, epsilon is set to
. The
expression |Z| is the absolute value of Z. The function
fabs, found in math.h, returns the absolute value of its argument.
Note that the call to newton passes a parameter, epsilon. In
the example driver, epsilon is set to 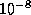 .
.