Project 1

Due September 26, 2000

1. Let x be a node and L be a list of nodes in ascending order of their values. A node is represented as a pair (name value), i.e., it is itself a list. Then a list of nodes is represented by a list of lists. Write a Lisp program to insert node x into L in such a way that the resultant list remains in ascending order of their nodes' values. After each insertion, list L is enlarged by on node.

Apply your program to the following data. Successively insert the following nodes

1) (b 5) 2) (e 20) 3) (f 1) 4) (g 6)

into the initial list L = ((a 2) (b 5) (c 10));

2. Write a LISP program to construct a binary search three of integers. A non-empty binary search tree can be represented by a list (root L1 L2), where root is an integer, and L1 and L2 are two subtrees whose nodes are less and great than the root, respectively. For example, a tree

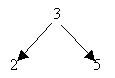
can be represented by list (3 (2 nil nil) (5 nil nil)) or (3 (2 () ()) (5 () ())).

The tree is constructed by successively inserting every element in a lisp (of integers) into the tree, which is initially represented as an empty list. Apply you program to construct a tree from the following list of integers: (10 5 8 28 3 15 6 3 18 21)

3. Let S1 and S2 be two S-expressions. Write a Lisp function which, taking S1 and S2 as its arguments, returns T if S1 appears in S2 and NIL, otherwise. This function sometimes is called a generalized membership function. (Note: S2 can be a complex, nested list.)

Apply your program to the following data:

1) S1 = a, S2 = ((b (c a) d) x (y (u v)))

2) S1 = (u v), S2 = ((b (c a) d) (y (u v)))