CS451 Selected Lecture Notes
Note that this file is plain text and .gif files. The plain text spells
out Greek letters because they can not be typed.
These are not intended to be complete lecture notes.
Complicated figures or tables or formulas are included here
in case they were not clear or not copied correctly in class.
Information from the language definitions, automata definitions,
computability definitions and class definitions is not duplicated here.
Lecture numbers correspond to the syllabus numbering.
Lecture 1 Fast Summary Part 1
Lecture 2 Fast Summary Part 2
Lecture 3 DFA and regular expressions
Lecture 4 Nondeterministic Finite Automata NFA
Lecture 5 NFA with epsilon moves
Lecture 6 regular expression to NFA
Lecture 7 NFA to regular expression, Moore, Mealy
Lecture 8 Pumping Lemma for regular languages
Lecture 9 Intersection of two languages, closure
Lecture 10 Decision Algorithms
Lecture 11 Quiz 1
Lecture 12 Myhill-Nerode minimization
Lecture 13 Formal Grammars, CFG
Lecture 14 Context Free Grammar derivation trees
Lecture 15 CFG 'simplification' algorithm
Lecture 16 Chomsky Normal Form
Lecture 17 Greibach Normal Form
Lecture 18 Inherently ambiguous CFL's, Project
Lecture 19 Quiz 2
Lecture 20 Push Down Automata
Lecture 21 CFL to PDA
Lecture 22 NPDA to CFL
Lecture 23 CYK algorithm for CFG's
Lecture 24 Pumping Lemma for Context Free Languages
Lecture 25 CFL closure properties
Lecture 26 Turing Machine Model
Lecture 27 The Halting Problem
Lecture 28 Church Turing Thesis
Lecture 29 Review
Lecture 30 Final Exam
Other Links
A fast summary of what will be covered in this course (part 1)
For reference, read through the automata definitions and
language definitions.
A fast summary of what will be covered in this course (part 2)
For reference, read through the computability definitions.
Example of a Deterministic Finite Automata, DFA
Machine Definition M = (Q, Sigma, alpha, q0, F)
Q = { q0, q1, q2, q3, q4 } the set of states
Sigma = { 0, 1 } the input string alphabet
q0 = q0 the starting state
F = { q2, q4 } the set of final states (accepting)
inputs
alpha | 0 | 1 |
---------+---------+---------+
q0 | q3 | q1 |
q1 | q1 | q2 |
states q2 | q2 | q2 |
q3 | q4 | q3 |
q4 | q4 | q4 |
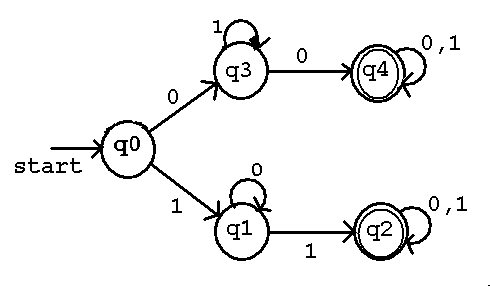
An exactly equivalent diagram description for the machine M.
L(M) is the notation for a Formal Language defined by a machine M.
Some of the shortest strings in L(M) = { 00, 11, 000, 001, 010, 101, 110, 111,
0000, 00001, ... }
Every input sequence goes through a sequence of states, for example
00 q0 q3 q4
11 q0 q1 q2
000 q0 q3 q4 q4
001 q0 q3 q4 q4
010 q0 q3 q3 q4
More information on DFA
Definition of a Regular Expression
A regular expression may be the null string,
r = epsilon
A regular expression may be an element of the input alphabet, sigma,
r = a
A regular expression may be the union of two regular expressions,
r = r1 + r2
A regular expression may be the concatenation (no symbol) of two
regular expressions,
r = r1 r2
A regular expression may be the Kleene closure (star) of a regular expression
r = r1* (the asterisk should be a superscript, but this is plain text)
A regular expression may be a regular expression in parenthesis
r = (r1)
Nothing is a regular expression unless it is constructed with only the
rules given above.
The language represented or generated by a regular expression is a
Regular Language, denoted L(r).
The regular expression for the machine M above is
r = (1(0*)1(0+1)*)+(0(1*)0(0+1)*)
For every DFA there is a regular language and for every regular language
there is a regular expression. Thus a DFA can be converted to a
regular expression and a regular expression can be converted to a DFA.
Example of a NFA, Nondeterministic Finite Automata given
by a) Machine Definition M = (Q, sigma, alpha, q0, F)
b) Equivalent regular expression
c) Equivalent diagram
and example tree of states for input string 0100011
and equivalent DFA, Deterministic Finite Automata for the first 3 states.
Machine Definition M = (Q, sigma, alpha, q0, F)
Q = { q0, q1, q2, q3, q4 } the set of states
F = { q2, q4 } the set of final states (accepting)
sigma = { 0, 1 } the input string alphabet
q0 = q0 the starting state
inputs
alpha | 0 | 1 |
---------+---------+---------+
q0 | {q0,q3} | {q0,q1} |
q1 | phi | {q2} |
states q2 | {q2} | {q2} |
q3 | {q4} | phi |
q4 | {q4} | {q4} |
The equivalent regular expression is (0+1)*(00+11)(0+1)*
defining L(M) is all strings over (0+1)* that have at least
one pair of zeros or one pair of ones.
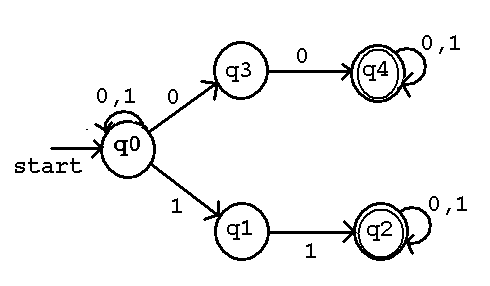
Equivalent NFA diagram.
The tree of states this NFA is in for the input 0100011
input
q0
/ \ 0
q3 q0
dies / \ 1
q1 q0
dies / \ 0
q3 q0
/ / \ 0
q4 q3 q0
/ / / \ 0
q4 q4 q3 q0
/ / dies / \ 1
q4 q4 q1 q0
/ / / / \ 1
q4 q4 q2 q1 q0
^ ^ ^
| | |
accepting paths in NFA tree
Construct a DFA equivalent to the NFA above using just the first
three rows of alpha.
The DFA machine is M' = (Q', sigma, alpha', q0', F')
Q' = 2**Q, the power set of Q = { phi, {q0}, {q1}, {q2}, {q0,q1}, {q0,q2},
{q1,q2}, {q0,q1,q2} }
Note: read the eight elements of the set Q' as names of states of M'
F' = { {q2}, {q0,q2}, {q1,q2}, {q0,q1,q2} }
sigma is the same
q0' = {q0}
inputs
alpha' | 0 | 1 |
----------+-------------+-------------+
phi | phi | phi | never reached
{q0} | {q0} | {q0,q1} |
{q1} | phi | {q2} | never reached
states {q2} | {q2} | {q2} | never reached
{q0,q1} | {q0} | {q0,q1,q2} |
{q0,q2} | {q0,q2} | {q0,q1,q2} | never reached
{q1,q2} | {q2} | {q2} | never reached
{q0,q1,q2} | {q0,q1,q2} | {q0,q1,q2} |
Note: Some of the states in the DFA may be unreachable
The alpha' was constructed directly from alpha.
Using the notation f'({q0},0) = f(q0,0) to mean:
in alpha' in state {q0} with input 0 go to the state
shown in alpha with input 0. Take the union of all such states.
Further notation, phi is the empty set so phi union the set A is just the set A.
Some samples: f'({q0,q1},0) = f(q0,0) union f(q1,0) = {q0}
f'({q0,q1},1) = f(q0,1) union f(q1,1) = {q0,q1,q2}
f'({q0,q2},0) = f(q0,0) union f(q2,0) = {q0,q2}
f'({q0,q2},1) = f(q0,1) union f(q2,1) = {q0,q1,q2}
The sequence of states is unique for a DFA, so for the same input as
above 0100011 the sequence of states is
{q0} 0 {q0} 1 {q0,q1} 0 {q0} 0 {q0} 0 {q0} 1 {q0,q1} 1 {q0,q1,q2}
This sequence does not have any states involving q3 or q4 because just
a part of the above NFA was converted to a DFA. This DFA does not
accept the string 00 whereas the NFA above does accept 00.
Definition and example of a NFA with epsilon transitions.
Remember, epsilon is the zero length string, so it can be any where
in the input string, front, back, between any symbols.
Then the conversion algorithm from a NFA with epsilon transitions to
a NFA without epsilon transitions.
Consider the NFA-epsilon move machine M = { Q, sigma, delta, q0, F}
Q = { q0, q1, q2 }
sigma = { a, b, c } and epsilon moves
q0 = q0
F = { q2 }
inputs
delta | a | b | c |epsilon
------+------+------+------+-------
q0 | {q0} | phi | phi | {q1}
------+------+------+------+-------
q1 | phi | {q2} | phi | {q2}
------+------+------+------+-------
q2 | phi | phi | {q2} | phi
------+------+------+------+-------
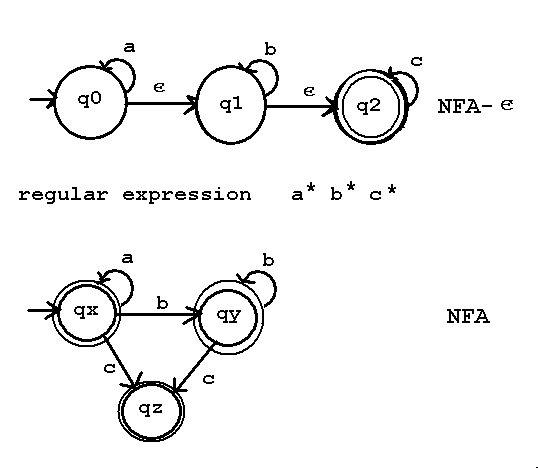
Now convert the NFA with epsilon moves to a NFA M = ( Q', sigma, delta', q0', F')
First determine the states of the new machine, Q' = the epsilon closure
of the states in the NFA with epsilon moves. There will be the same number
of states but the names can be constructed by writing the state name as
the set of states in the epsilon closure. The epsilon closure is the
initial state and all states that can be reached by one or more epsilon moves.
Thus q0 in the NFA-epsilon becomes {q0,q1,q2} because the machine can move
from q0 to q1 by an epsilon move, then check q1 and find that it can move
from q1 to q2 by an epsilon move.
q1 in the NFA-epsilon becomes {q1,q2} because the machine can move from
q1 to q2 by an epsilon move.
q2 in the NFA-epsilon becomes {q2} just to keep the notation the same. q2
can go nowhere except q2, that is what phi means, on an epsilon move.
We do not show the epsilon transition of a state to itself here, but,
beware, we will take into account the state to itself epsilon transition
when converting NFA's to regular expressions.
The initial state of our new machine is {q0,q1,q2} the epsilon closure of q0
The final state(s) of our new machine is the new state(s) that contain
a state symbol that was a final state in the original machine.
The new machine accepts the same language as the old machine, thus same sigma.
So far we have for out new NFA
Q' = { {q0,q1,q2}, {q1,q2}, {q2} } or renamed { qx, qy, qz }
sigma = { a, b, c }
F' = { {q0,q1,q2}, {q1,q2}, {q2} } or renamed { qx, qy, qz }
q0 = {q0,q1,q2} or renamed qx
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | | |
------------+--------------+--------------+--------------
qy or {q1,q2} | | |
------------+--------------+--------------+--------------
qz or {q2} | | |
------------+--------------+--------------+--------------
Now we fill in the transitions. Remember that a NFA has transition entries
that are sets. Further, the names in the transition entry sets must be
only the state names from Q'.
Very carefully consider each old machine transitions in the first row.
You can ignore any "phi" entries and ignore the "epsilon" column.
In the old machine delta(q0,a)=q0 thus in the new machine
delta'({q0,q1,q2},a)={q0,q1,q2} this is just because the new machine
accepts the same language as the old machine and must at least have the
the same transitions for the new state names.
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | |
------------+--------------+--------------+--------------
qy or {q1,q2} | | |
------------+--------------+--------------+--------------
qz or {q2} | | |
------------+--------------+--------------+--------------
No more entries go under input a in the first row because
old delta(q1,a)=phi, delta(q2,a)=phi
Now consider the input b in the first row, delta(q0,b)=phi, delta(q1,phi)={q1}
and delta(q2,b)=phi. The reason we considered q0, q1 and q2 in the old
machine was because out new state has symbols q0, q1 and q2 in the new
state name from the epsilon closure. Since q1 is in {q0,q1,q2} and
delta(q1,b)=q1 then delta'({q0,q1,q2},b)={q1,q2}. WHY {q1,q2} ?, because
{q1,q2} is the new machines name for the old machines name q1. Just
compare the zeroth column of delta to delta'. So we have
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | {{q1,q2}} |
------------+--------------+--------------+--------------
qy or {q1,q2} | | |
------------+--------------+--------------+--------------
qz or {q2} | | |
------------+--------------+--------------+--------------
Now, because our new qx state has a symbol q2 in its name and
delta(q2,c)=q2 is in the old machine, the new name for the old q2,
which is qz or {q2} is put into the input c transition in row 1.
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | {{q1,q2}} | {{q2}} or qz
------------+--------------+--------------+--------------
qy or {q1,q2} | | |
------------+--------------+--------------+--------------
qz or {q2} | | |
------------+--------------+--------------+--------------
Now, tediously, move on to row two, ... .
You are considering all transitions in the old machine, delta,
for all old machine state symbols in the name of the new machines states.
Fine the old machine state that results from an input and translate
the old machine state to the corresponding new machine state name and
put the new machine state name in the set in delta'. Below are the
"long new state names" and the renamed state names in delta'.
inputs
delta' | a | b | c
------------+--------------+--------------+--------------
qx or {q0,q1,q2} | {{q0,q1,q2}} | {{q1,q2}} | {{q2}} or {qz}
------------+--------------+--------------+--------------
qy or {q1,q2} | phi | {{q1,q2}} | {{q2}} or {qz}
------------+--------------+--------------+--------------
qz or {q2} | phi | phi | {{q2}} or {qz}
------------+--------------+--------------+--------------
inputs
delta' | a | b | c <-- input alphabet sigma
---+------+------+-----
/ qx | {qx} | {qy} | {qz}
/ ---+------+------+-----
Q' qy | phi | {qy} | {qz}
\ ---+------+------+-----
\ qz | phi | phi | {qz}
---+------+------+-----
Given a regular expression there is an associated regular language L(r).
Since there is a finite automata for every regular language,
there is a machine, M, for every regular expression such that L(M) = L(r).
The constructive proof provides an algorithm for constructing a machine, M,
from a regular expression r. The six constructions below correspond to
the cases:
1) The entire regular expression is the null string, i.e. L={epsilon}
r = epsilon
2) The entire regular expression is empty, i.e. L=phi r = phi
3) An element of the input alphabet, sigma, is in the regular expression
r = a where a is an element of sigma.
4) Two regular expressions are joined by the union operator, +
r1 + r2
5) Two regular expressions are joined by concatenation (no symbol)
r1 r2
6) A regular expression has the Kleene closure (star) applied to it
r*
The construction proceeds by using 1) or 2) if either applies.
The construction first converts all symbols in the regular expression
using construction 3).
Then working from inside outward, left to right at the same scope,
apply the one construction that applies from 4) 5) or 6).
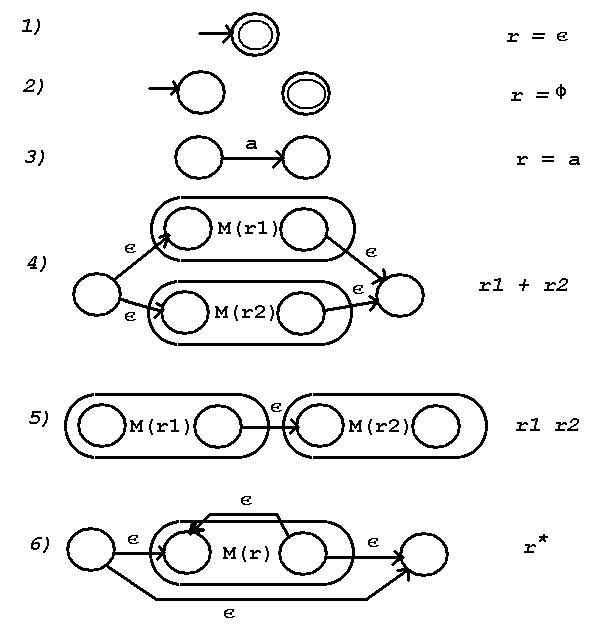The result is a NFA with epsilon moves. This NFA can then be converted
to a NFA without epsilon moves. Further conversion can be performed to
get a DFA. All these machines have the same language as the
regular expression from which they were constructed.
The construction covers all possible cases that can occur in any
regular expression. Because of the generality there are many more
states generated than are necessary. The unnecessary states are
joined by epsilon transitions. Very careful compression may be
performed. For example, the fragment regular expression aba would be
a e b e a
q0 ---> q1 ---> q2 ---> q3 ---> q4 ---> q5
with e used for epsilon, this can be trivially reduced to
a b a
q0 ---> q1 ---> q2 ---> q3
A careful reduction of unnecessary states requires use of the
Myhill-Nerode Theorem of section 3.4. This will provide a DFA
that has the minimum number of states.
Conversion of a NFA to a regular expression was started in this
lecture and finished in the next lecture. The notes are in lecture 7.
Conversion algorithm from a NFA to a regular expression.
Start with the transition table for the NFA with the following
state naming conventions:
the first state is 1 or q1 or s1 which is the starting state.
states are numbered consecutively, 1, 2, 3, ... n
The transition table is a typical NFA where the table entries
are sets of states and phi the empty set is allowed.
The set F of final states must be known.
We call the variable r a regular expression.
We can talk about r being the regular expression with i,j subscripts
ij
Note r is just a (possibly) different regular expression from r
12 53
Because we need multiple columns in a table we are going to build, we
also use a superscript in the naming of regular expression.
1 3 k k-1
r r r r are just names of different regular expressions
12 64 1k ij
2
We are going to build a table with n rows and n+1 columns labeled
| k=0 | k=1 | k=2 | ... | k=n
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | | n
r | r | r | r | ... | r Only build column n
11 | 11 | 11 | 11 | | 11 for 1,final state
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | | n The final regular expression
r | r | r | r | ... | r is then the union, +, of
12 | 12 | 12 | 12 | | 12 the column n
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | | n
r | r | r | r | ... | r
13 | 13 | 13 | 13 | | 13
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | |
r | r | r | r | ... |
21 | 21 | 21 | 21 | |
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | |
r | r | r | r | ... |
22 | 22 | 22 | 22 | |
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | |
r | r | r | r | ... |
23 | 23 | 23 | 23 | |
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | |
r | r | r | r | ... |
31 | 31 | 31 | 31 | |
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | |
r | r | r | r | ... |
32 | 32 | 32 | 32 | |
----+--------+-------+-------+-----+------
| 0 | 1 | 2 | |
r | r | r | r | ... |
33 | 33 | 33 | 33 | |
^ 2
|- Note n rows, all pairs of numbers from 1 to n
Now, build the table entries for the k=0 column:
/
0 / +{ x | delta(q ,x) = q } i /= j
r = / i j
ij \
\ +{ x | delta(q ,x) = q } + epsilon i = j
\ i i
where delta is the transition table function,
x is some symbol from sigma
the q's are states
0
r could be phi, epsilon, a, 0+1, or a+b+d+epsilon
ij
notice there are no Kleene Star or concatenation in this column
Next, build the k=1 column:
1 0 0 * 0 0
r = r ( r ) r + r note: all items are from the previous column
ij i1 11 1j ij
Next, build the k=2 column:
2 1 1 * 1 1
r = r ( r ) r + r note: all items are from the previous column
ij i2 22 2j ij
Then, build the rest of the k=k columns:
k k-1 k-1 * k-1 k-1
r = r ( r ) r + r note: all items are from previous column
ij ik kk kj ij
Finally, for final states p, q, r the regular expression is
n n n
r + r + r
1p 1q 1r
Note that this is from a constructive proof that every NFA has a language
for which there is a corresponding regular expression.
Some minimization rules for regular expressions
These can be applied at every step.
Note: phi is the empty set
epsilon is the zero length string
0, 1, a, b, c, are symbols in sigma
x is a variable or regular expression
( ... )( ... ) is concatenation
( ... ) + ( ... ) is union
( ... )* is the Kleene Closure = Kleene Star
(phi)(x) = (x)(phi) = phi
(epsilon)(x) = (x)(epsilon) = x
(phi) + (x) = (x) + (phi) = x
x + x = x
(epsilon)* = (epsilon)(epsilon) = epsilon
(x)* + (epsilon) = (x)* = x*
(x + epsilon)* = x*
x* (a+b) + (a+b) = x* (a+b)
x* y + y = x* y
(x + epsilon)x* = x* (x + epsilon) = x*
(x+epsilon)(x+epsilon)* (x+epsilon) = x*
Now for an example:
Given M=(Q, sigma, delta, q0, F) as
delta | a | b | c Q = { q1, q2}
--------+------+------+----- sigma = { a, b, c }
q1 | {q2} | {q2} | {q1} q0 = q1
--------+------+------+----- F = { q2}
q2 | phi | phi | phi
--------+------+------+-----
| k=0 | k=1 (using e for epsilon)
-----+-------------+------------------------------------
r | c + epsilon | (c+e)(c+e)* (c+e) + (c+e) = c*
11 | |
-----+-------------+------------------------------------
r | a + b | (c+e)(c+e)* (a+b) + (a+b) = c* (a+b)
12 | |
-----+-------------+------------------------------------
r | phi | phi (c+e)* (c+e) + phi = phi
21 | |
-----+-------------+------------------------------------
r | epsilon | phi (c+e)* (a+b) + e = e
22 | |
-----+-------------+------------------------------------
| k=0 | k=1 | k=2 (using e for epsilon)
-----+-------------+----------+-------------------------
r | c + epsilon | c* |
11 | | |
-----+-------------+----------+-------------------------
r | a + b | c* (a+b) | (a+b)(e)* (e) + c* (a+b) only final state
12 | | |
-----+-------------+----------+-------------------------
r | phi | phi |
21 | | |
-----+-------------+----------+-------------------------
r | epsilon | e |
22 | | |
-----+-------------+----------+-------------------------
the final regular expression minimizes to c* (a+b)
Additional topics include Moore Machines and
Mealy Machines
The Pumping Lemma is generally used to prove a language is not regular.
If a DFA, NFA or NFA-epsilon machine can be constructed to exactly accept
a language, then the language is a Regular Language.
If a regular expression can be constructed to exactly generate the
strings in a language, then the language is regular.
To prove a language is not regular requires a specific definition of
the language and the use of the Pumping Lemma for Regular Languages.
A note about proofs using the Pumping Lemma:
Given: Formal statements A and B.
A implies B.
If you can prove B is false, then you have proved A is false.
For the Pumping Lemma, the statement "A" is "L is a Regular Language",
The statement "B" is a statement from the Predicate Calculus.
(This is a plain text file that uses words for the upside down A that
reads 'for all' and the backwards E that reads 'there exists')
Formal statement of the Pumping Lemma:
L is a Regular Language implies
(there exists n)(for all z)[z in L and |z|>=n implies
{(there exists u,v,w)(z = uvw and |uv|<=n and |v|>1 and
i
(for all i>=0)(uv w is in L) )}]
The two commonest ways to use the Pumping Lemma to prove a language
is NOT regular are:
a) show that there is no possible n for the (there exists n),
this is usually accomplished by showing a contradiction such
as (n+1)(n+1) < n*n+n
b) show there is no way to partition z into u, v and w such that
i
uv w is in L, typically for a value i=0 or i=2.
Be sure to cover all cases by argument or enumerating cases.
A class of languages is simply a set of languages with some
property that determines if a language is in the class (set).
The class of languages called regular languages is the set of all
languages that are regular. Remember, a language is regular if it is
accepted by some DFA, NFA, NFA-epsilon or regular expression.
A single language is a set of strings over a finite alphabet and
is therefor countable. A regular language may have an infinite
number of strings. The strings of a regular language can be enumerated,
written down for length 0, length 1, length 2 and so forth.
But, the class of regular languages is the size of a power set
of any given regular language. This comes from the fact that
regular languages are closed under union. From mathematics we
know a power set of a countable set is not countable. A set that
is not countable, like the real numbers, can not be enumerated.
A class of languages is closed under some operation, op, when for any
two languages in the class, say L1 and L2, L1 op L2 is in the class.
We have seen that regular languages are closed under union because
the "+" is regular expressions yields a union operator for regular
languages. Similarly, for DFA machines, L(M1) union L(M2) is
L(M1 union M2) by the construction in lecture 6.
Thus we know the set of regular languages is closed under union.
In symbolic terms, L1 and L2 regular languages and L3 = L1 union L2
implies L3 is a regular language.
The complement of a language is defined in terms of set difference
__
from sigma star. L1 = sigma * - L1. The language L1 bar, written
as L1 with a bar over it, has all strings from sigma star except
the strings in L1. Sigma star is all possible strings over the
alphabet sigma. It turns out a DFA for a language can be made a
DFA for the complement language by changing all final states to
not final states and visa versa. (Warning! This is not true for NFA's)
Thus regular languages are closed under complementation.
Given union and complementation, by DeMorgan's Theorem,
L1 and L2 regular languages and L3 = L1 intersect L2 implies
______________
__ __
L3 is a regular language. L3 = ( L1 union L2) .
The construction of a DFA, M3, such that L(M3) = L(M1) intersect L(M2)
is given by:
Let M1 = (Q1, sigma, delta1, q1, F1)
Let M2 = (Q2, sigma, delta2, q2, F2)
Let S1 x S2 mean the cross product of sets S1 and S2, all ordered pairs,
Then
M3 = (Q1 x Q2, sigma, delta3, [q1,q2], F1 x F2)
where [q1,q2] is an ordered pair from Q1 x Q2,
delta3 is constructed from
delta3([x1,x2],a) = [delta1(x1,a), delta2(x2,a)] for all a in sigma
and all [x1,x2] in Q1 x Q2.
We choose to say the same alphabet is used in both machines, but this
works in general by picking the alphabet of M3 to be the intersection
of the alphabets of M1 and m2 and using all 'a' from this set.
Regular set properties:
One way to show that an operation on two regular languages produces a
regular language is to construct a machine that performs the operation.
Remember, the machines have to be DFA, NFA or NFA-epsilon type machines
because these machines have corresponding regular languages.
Consider two machines M1 and M2 for languages L1(M1) and L2(M2).
To show that L1 intersect L2 = L3 and L3 is a regular language we
construct a machine M3 and show by induction that M3 only accepts
strings that are in both L1 and L2.
M1 = (Q1, Sigma, delta1, q1, F1) with the usual definitions
M2 = (Q2, Sigma, delta2, q2, F2) with the usual definitions
Now construct M3 = (Q3, Sigma, delta3, q3, F3) defined as
Q3 = Q1 x Q2 set cross product
q3 = [q1,q2] q3 is an element of Q3, the notation means an ordered pair
Sigma = Sigma = Sigma we choose to use the same alphabet,
else some fix up is required
F3 = F1 x F2 set cross product
delta3 is constructed from
delta3([qi,qj],x) = [delta1(qi,x),delta2(qj,x)]
as you might expect, this is most easily
performed on a DFA
The language L3(M3) is shown to be the intersection of L1(M1) and L2(M2)
by induction on the length of the input string.
For example:
M1: Q1 = {q0, q1}, Sigma = {a, b}, delta1, q1=q0, F1 = {q1}
M2: Q2 = {q3, q4, q5}, Sigma = {a, b}, delta2, q2=q3, F2 = {q4,q5}
delta1 | a | b | delta2 | a | b |
---+----+----+ -----+----+----+
q0 | q0 | q1 | q3 | q3 | q4 |
---+----+----+ -----+----+----+
q1 | q1 | q1 | q4 | q5 | q3 |
---+----+----+ -----+----+----+
q5 | q5 | q5 |
-----+----+----+
M3 now is constructed as
Q3 = Q1 x Q2 = {[q0,q3], [q0,q4], [q0,q5], [q1,q3], [q1,q4], [q1,q5]}
F3 = F1 x F2 = {[q1,q4], [q1,q5]}
initial state q3 = [q0,q3]
Sigma = technically Sigma_1 intersect Sigma_2
delta3 is constructed from delta3([qi,qj],x) = [delta1(qi,x),delta2(qj,x)]
delta3 | a | b |
---------+---------+---------+
[q0,q3] | [q0,q3] | [q1,q4] | this is a DFA when both
---------+---------+---------+ M1 and M2 are DFA's
[q0,q4] | [q0,q5] | [q1,q3] |
---------+---------+---------+
[q0,q5] | [q0,q5] | [q1,q5] |
---------+---------+---------+
[q1,q3] | [q1,q3] | [q1,q4] |
---------+---------+---------+
[q1,q4] | [q1,q5] | [q1,q3] |
---------+---------+---------+
[q1,q5] | [q1,q5] | [q1,q5] |
---------+---------+---------+
As we have seen before there may be unreachable states.
In this example [q0,q4] and [q0,q5] are unreachable.
It is possible for the intersection of L1 and L2 to be empty,
thus a final state will never be reachable.
Coming soon, the Myhill-Nerode theorem and minimization to
eliminate useless states.
Mostly review for the quiz.
On paper, graded and returned.
Myhill-Nerode theorem and minimization to eliminate useless states.
The Myhill-Nerode Theorem says the following three statements are equivalent:
1) The set L, a subset of Sigma star, is accepted by a DFA.
(We know this means L is a regular language.)
2) L is the union of some of the equivalence classes of a right
invariant(with respect to concatenation) equivalence relation
of finite index. The "some of" will relate to Final states.
3) Let equivalence relation RL be defined by: xRLy if and only if
for all z in Sigma star, xz is in L exactly when yz is in L.
Then RL is of finite index.
The notation RL means an equivalence relation R over the language L.
The notation RM means an equivalence relation R over a machine M.
We know for every regular language L there is a machine M that
exactly accepts the strings in L.
Think of an equivalence relation as being true or false for a
specific pair of strings x and y. Thus xRy is true for some
set of pairs x and y. We will use a relation R such that
xRy <=> yRx x has a relation to y if and only if y has
the same relation to x. This is known as symmetric.
xRy and yRz implies xRz. This is known as transitive.
xRx is true. This is known as reflexive.
Our RL is defined xRLy <=> for all z in Sigma star (xz in L <=> yz in L)
Our RM is defined xRMy <=> xzRMyz for all z in Sigma star.
In other words delta(q0,xz) = delta(delta(q0,x),z)=
delta(delta(q0,y),z) = delta(q0,yz)
for x, y and z strings in Sigma star.
RM divides the set Sigma star into equivalence classes, one class for
each state reachable in M from the starting state q0. To get RL from
this we have to consider only the Final reachable states of M.
From this theorem comes the provable statement that there is a
smallest, fewest number of states, DFA for every regular language.
The labeling of the states is not important, thus the machines
are the same within an isomorphism. (iso=constant, morph=change)
Now for the algorithm that takes a DFA, we know how to reduce a NFA
or NFA-epsilon to a DFA, and produces a minimum state DFA.
-3) Start with a machine M = (Q, Sigma, delta, q0, F) as usual
-2) Remove from Q, F and delta all states that can not be reached from q0.
Remember a DFA is a directed graph with states as nodes. Thus us
a depth first search to mark all the reachable states. The unreachable
states, if any, are then eliminated and the algorithm proceeds.
-1) Build a two dimensional matrix labeling the right side q0, q1, ...
running down and denote this as the "p" first subscript.
Label the top as q0, q1, ... and denote this as the "q" second subscript
0) Put dashes in the major diagonal and the lower triangular part
of the matrix (everything below the diagonal). we will always use the
upper triangular part because xRMy = yRMx is symmetric. We will also
use (p,q) to index into the matrix with the subscript of the state
called "p" always less than the subscript of the state called "q".
We can have one of three things in a matrix location where there is
no dash. An X indicates a distinct state from our initialization
in step 1). A link indicates a list of matrix locations
(pi,qj), (pk,ql), ... that will get an x if this matrix location
ever gets an x. At the end, we will label all empty matrix locations
with a O. (Like tic-tac-toe) The "O" locations mean the p and q are
equivalent and will be the same state in the minimum machine.
(This is like {p,q} when we converted a NFA to a DFA. and is
the transitive closure just like in NFA to DFA.)
NOW FINALLY WE ARE READY for Page 70, Figure 3.8.
1) For p in F and q in Q-F put an "X" in the matrix at (p,q)
This is the initialization step. Do not write over dashes.
These matrix locations will never change. An X or x at (p,q)
in the matrix means states p and q are distinct in the minimum
machine. If (p,q) has a dash, put the X in (q,p)
2) BIG LOOP TO END
For every pair of distinct states (p,q) in F X F do 3) through 7)
and for every pair of distinct states (p,q)
in (Q-F) x (Q-F) do 3) through 7)
(Actually we will always have the index of p < index of q and
p never equals q so we have fewer checks to make.)
3) 4) 5)
If for any input symbol 'a', (r,s) has an X or x then put an x at (p,q)
Check (s,r) if (r,s) has a dash. r=delta(p,a) and s=delta(q,a)
Also, if a list exists for (p,q) then mark all (pi,qj) in the list
with an x. Do it for (qj,pi) if (pi,qj) has a dash. You do not have
to write another x if one is there already.
6) 7)
If the (r,s) matrix location does not have an X or x, start a list
or add to the list (r,s). Of course, do not do this if r = s,
of if (r,s) is already on the list. Change (r,s) to (s,r) if
the subscript of the state r is larger than the subscript of the state s
END BIG LOOP
Now for an example, non trivial, where there is a reduction.
M = (Q, Sigma, delta, q0, F} and we have run a depth first search to
eliminate states from Q, F and delta that can not be reached from q0.
picture of machine
Q = {q0, q1, q2, q3, q4, q5, q6, q7, q8}
Sigma = {a, b}
q0 = q0
F = {q2, q3, q5, q6}
delta | a | b | note Q-F = {q0, q1, q4, q7, q8}
----+----+----+
q0 | q1 | q4 | We use an ordered F x F = {(q2, q3),
----+----+----+ (q2, q5),
q1 | q2 | q3 | (q2, q6),
----+----+----+ (q3, q5),
q2 | q7 | q8 | (q3, q6),
----+----+----+ (q5, q6)}
q3 | q8 | q7 |
----+----+----+ We use an ordered (Q-F) x (Q-F) = {(q0, q1),
q4 | q5 | q6 | (q0, q4),
----+----+----+ (q0, q7),
q5 | q7 | q8 | (q0, q8),
----+----+----+ (q1, q4),
q6 | q7 | q8 | (q1, q7),
----+----+----+ (q1, q8),
q7 | q7 | q7 | (q4, q7),
----+----+----+ (q4, q8),
q8 | q8 | q8 | (q7, q8)}
----+----+----+
Now, build the matrix labeling the "p" rows q0, q1, ...
and labeling the "q" columns q0, q1, ...
and put in dashes on the diagonal and below the diagonal
q0 q1 q2 q3 q4 q5 q6 q7 q8
+---+---+---+---+---+---+---+---+---+
q0 | - | | | | | | | | |
+---+---+---+---+---+---+---+---+---+
q1 | - | - | | | | | | | |
+---+---+---+---+---+---+---+---+---+
q2 | - | - | - | | | | | | |
+---+---+---+---+---+---+---+---+---+
q3 | - | - | - | - | | | | | |
+---+---+---+---+---+---+---+---+---+
q4 | - | - | - | - | - | | | | |
+---+---+---+---+---+---+---+---+---+
q5 | - | - | - | - | - | - | | | |
+---+---+---+---+---+---+---+---+---+
q6 | - | - | - | - | - | - | - | | |
+---+---+---+---+---+---+---+---+---+
q7 | - | - | - | - | - | - | - | - | |
+---+---+---+---+---+---+---+---+---+
q8 | - | - | - | - | - | - | - | - | - |
+---+---+---+---+---+---+---+---+---+
Now fill in for step 1) (p,q) such that p in F and q in (Q-F)
{ (q2, q0), (q2, q1), (q2, q4), (q2, q7), (q2, q8),
(q3, q0), (q3, q1), (q3, q4), (q3, q7), (q3, q8),
(q5, q0), (q5, q1), (q5, q4), (q5, q7), (q5, q8),
(q6, q0), (q6, q1), (q6, q4), (q6, q7), (q6, q8)}
q0 q1 q2 q3 q4 q5 q6 q7 q8
+---+---+---+---+---+---+---+---+---+
q0 | - | | X | X | | X | X | | |
+---+---+---+---+---+---+---+---+---+
q1 | - | - | X | X | | X | X | | |
+---+---+---+---+---+---+---+---+---+
q2 | - | - | - | | X | | | X | X |
+---+---+---+---+---+---+---+---+---+
q3 | - | - | - | - | X | | | X | X |
+---+---+---+---+---+---+---+---+---+
q4 | - | - | - | - | - | X | X | | |
+---+---+---+---+---+---+---+---+---+
q5 | - | - | - | - | - | - | | X | X |
+---+---+---+---+---+---+---+---+---+
q6 | - | - | - | - | - | - | - | X | X |
+---+---+---+---+---+---+---+---+---+
q7 | - | - | - | - | - | - | - | - | |
+---+---+---+---+---+---+---+---+---+
q8 | - | - | - | - | - | - | - | - | - |
+---+---+---+---+---+---+---+---+---+
Now fill in more x's by checking all the cases in step 2)
and apply steps 3) 4) 5) 6) and 7). Finish by filling in blank
matrix locations with "O".
For example (r,s) = (delta(p=q0,a), delta(q=q1,a)) so r=q1 and s= q2
Note that (q1,q2) has an X, thus (q0, q1) gets an "x"
Another from F x F (r,s) = (delta(p=q4,b), delta(q=q5,b)) so r=q6 and s=q8
thus since (q6, q8) has an X then (p,q) = (q4,q5) gets an "x"
It depends on the order of the choice of (p, q) in step 2) whether
a (p, q) gets added to a list in a cell or gets an "x".
Another (r,s) = (delta(p,a), delta(q,a)) where p=q0 and q=q8 then
s = delta(q0,a) = q1 and r = delta(q8,a) = q8 but (q1, q8) is blank.
Thus start a list in (q1, q8) and put (q0, q8) in this list.
[ This is what 7) says: put (p, q) on the list for (delta(p,a), delta(q,a))
and for our case the variable "a" happens to be the symbol "a".]
Eventually (q1, q8) will get an "x" and the list, including (q0, q8)
will get an "x'.
Performing the tedious task results in the matrix:
q0 q1 q2 q3 q4 q5 q6 q7 q8
+---+---+---+---+---+---+---+---+---+
q0 | - | x | X | X | x | X | X | x | x |
+---+---+---+---+---+---+---+---+---+
q1 | - | - | X | X | O | X | X | x | x | The "O" at (q1, q4) means {q1, q4}
+---+---+---+---+---+---+---+---+---+ is a state in the minimum machine
q2 | - | - | - | O | X | O | O | X | X |
+---+---+---+---+---+---+---+---+---+
q3 | - | - | - | - | X | O | O | X | X | The "O" for (q2, q3), (q2, q5) and
+---+---+---+---+---+---+---+---+---+ (q2, q6) means they are one state
q4 | - | - | - | - | - | X | X | x | x | {q2, q3, q5, q6} in the minimum
+---+---+---+---+---+---+---+---+---+ machine. many other "O" just
q5 | - | - | - | - | - | - | O | X | X | confirm this.
+---+---+---+---+---+---+---+---+---+
q6 | - | - | - | - | - | - | - | X | X |
+---+---+---+---+---+---+---+---+---+
q7 | - | - | - | - | - | - | - | - | O | The "O" in (q7, q8) means {q7, q8}
+---+---+---+---+---+---+---+---+---+ is one state in the minimum machine
q8 | - | - | - | - | - | - | - | - | - |
+---+---+---+---+---+---+---+---+---+
The resulting minimum machine is M' = (Q', Sigma, delta', q0', F')
with Q' = { {q0}, {q1,q4}, {q2,q3,q5,q6}, {q7,q8} } four states
F' = { {q2,q3,q5,q6} } only one final state
q0' = q0
delta' | a | b |
----------+----------------+------------------+
{q0} | {q1,q4} | {q1,q4} |
----------+----------------+------------------+
{q1,q4} | {q2,q3,q5,q6} | {q2,q3,q5,q6} |
----------+----------------+------------------+
{q2,q3,q5,q6} | {q7,q8} | {q7,q8} |
----------+----------------+------------------+
{q7,q8} | {q7,q8} | {q7,q8} |
----------+----------------+------------------+
Note: Fill in the first column of states first. Check that every
state occurs in some set and in only one set. Since this is a DFA
the next columns must use exactly the state names found in the
first column. e.g. q0 with input "a" goes to q1, but q1 is now {q1,q4}
Use the same technique as was used to convert a NFA to a DFA, but
in this case the result is always a DFA even though the states have
the strange looking names that appear to be sets, but are just
names of the states in the DFA.
picture of machine
It is possible for the entire matrix to be "X" or "x" at the end.
In this case the DFA started with the minimum number of states.
Grammars that have the same languages as DFA's
A grammar is defined as G = (V, T, P, S) where
V is a set of variables. We usually use capital letters for variables.
T is a set of terminal symbols. This is the same as Sigma for a machine.
P is a list of productions (rules) of the form:
variable -> concatenation of variables and terminals
S is the starting variable. S is in V.
A string z is accepted by a grammar G if some sequence of rules from P
can be applied to z with a result that is exactly the variable S.
We say that L(G) is the language generated (accepted) by the grammar G.
To start, we restrict the productions P to be of the form
A -> w w is a concatenation of terminal symbols
B -> wC w is a concatenation of terminal symbols
A, B and C are variables in V
and thus get a grammar that generates (accepts) a regular language.
Suppose we are given a machine M = (Q, Sigma, delta, q0, F) with
Q = { S }
Sigma = { 0, 1 }
q0 = S
F = { S }
delta | 0 | 1 |
---+---+---+
S | S | S |
---+---+---+
this looks strange because we would normally use q0 is place of S
The regular expression for M is (0+1)*
We can write the corresponding grammar for this machine as
G = (V, T, P, S) where
V = { S } the set of states in the machine
T = { 0, 1 } same as Sigma for the machine
P =
S -> epsilon | 0S | 1S
S = S the q0 state from the machine
the construction of the rules for P is directly from M's delta
If delta has an entry from state S with input symbol 0 go to state S,
the rule is S -> 0S.
If delta has an entry from state S with input symbol 1 go to state S,
the rule is S -> 1S.
There is a rule generated for every entry in delta.
delta(qi,a) = gj yields a rule qi -> a qj
An additional rule is generated for each final state, i.e. S -> epsilon
The shorthand notation S -> epsilon | 0S | 1S is the same as writing
the three rules. Read "|" as "or".
Grammars can be more powerful (read accept a larger class of languages)
than finite state machines (DFA's NFA's NFA-epsilon regular expressions).
i i
For example the language L = { 0 1 | i=0, 1, 2, ... } is not a regular
language. Yet, this language has a simple grammar
S -> epsilon | 0S1
Note that this grammar violates the restriction needed to make the grammars
language a regular language, i.e. rules can only have terminal symbols
and then one variable. This rule has a terminal after the variable.
A grammar for matching parenthesis might be
G = (V, T, P, S)
V = { S }
T = { ( , ) }
P = S -> epsilon | (S) | SS
S = S
We can check this be rewriting an input string
( ( ( ) ( ) ( ( ) ) ) )
( ( ( ) ( ) ( S ) ) ) S -> (S) where the inside S is epsilon
( ( ( ) ( ) S ) ) S -> (S)
( ( ( ) S S ) ) S -> (S) where the inside S is epsilon
( ( ( ) S ) ) S -> SS
( ( S S ) ) S -> (S) where the inside S is epsilon
( ( S ) ) S -> SS
( S ) S -> (S)
S S -> (S)
Thus the string ((()()(()))) is accepted by G because the rewriting
produced exactly S, the start variable..
The goal here is to take an arbitrary Context Free Grammar
G = (V, T, P, S) and perform transformations on the grammar that
preserve the language generated by the grammar but reach a
specific format for the productions.
Overview: Step 1a) Eliminate useless variables that can not become terminals
Step 1b) Eliminate useless variables that can not be reached
Step 2) Eliminate epsilon productions
Step 3) Eliminate unit productions
Step 4) Make productions Chomsky Normal Form
Step 5) Make productions Greibach Normal Form
Chomsky Normal Form is used by the CYK algorithm to determine
if a string is accepted by a Context Free Grammar.
Step 4) in the overall grammar "simplification" process is
to convert the grammar to Chomsky Normal Form.
Productions can be one of two formats A -> a or A -> BC
The right side of the production is either exactly
one terminal symbol or exactly two variables.
The grammars must have the "simplification" steps 1), 2) and 3) out
of the way, that is 1) No useless variables, 2) No nullable variables and
3) no unit productions.
Step 4) of "simplification" is the following algorithm:
'length' refers to the number of variables plus terminal
symbols on the right side of a production.
Loop through the productions
For each production with length greater than 1 do
Replace each terminal symbol with a new variable and
add a production new variable -> terminal symbol.
Loop through the productions
For each production with length grater than 2 do
Replace two rightmost variables with a new variable and
add a production new variable -> two rightmost variables.
(Repeat - either on a production or loop until no replacements.)
Now the grammar, as represented by the productions, is in Chomsky
Normal Form. proceed with CYK.
An optimization is possible but not required, for any two productions
with the same right side, delete the second production and
replace all occurrences of the second productions left variable
with the left variable of the first production in all productions.
Example grammar:
G = (V, T, P, S) V={S,A} T={a,b} S=S
S -> aAS
S -> a
A -> SbA
A -> SS
A -> ba
First loop through productions (Check n>1)
S -> aAS becomes S -> BAS (B is the next unused variable name)
B -> a
S -> a stays S -> a
A -> SbA becomes A -> SCA (C is the next unused variable name)
C -> b
A -> SS stays A -> SS
A -> ba becomes A -> DE
D -> b
E -> a
Second loop through productions (Check n>2)
S -> BAS becomes S -> BF (F is the next unused variable)
F -> AS
B -> a stays B -> a
S -> a stays S -> a
A -> SCA becomes A -> SG
G -> CA
C -> b stays C -> b
A -> SS stays A -> SS
A -> DE stays A -> DE
D -> b stays D -> b
E -> a stays E -> a
Optimization is possible, B -> a, S -> a, E -> a can be replaced
by the single production S -> a (just to keep 'S')
and all occurrences of 'B' and 'E' get replaced by 'S'.
Similarly D -> b can be deleted, keeping the C -> b production and
substituting 'C' for 'D'.
Giving the reduced Chomsky Normal Form:
S -> SF
F -> AS
S -> a
A -> CG
G -> CA
C -> b
A -> SS
A -> CS
Greibach Normal Form of a CFG has all productions of the form
A ->aV Where 'A' is a variable, 'a' is exactly one terminal and
'V' is a string of none or more variables.
Every CFG can be rewritten in Greibach Normal Form.
This is step 5 in the sequence of "simplification" steps for CFG's.
Greibach Normal Form will be used to construct a PushDown Automata
that recognizes the language generated by a Context Free Grammar.
Starting with Chomsky Normal Form ( A->BC or A->a ) ...
see book page 94, section 4.6
See project description
A CFL that is inherently ambiguous is one for which no
unambiguous CFG can exists.
i i j j i j j i
L= {a b c d | i,j>0} union {a b c d | i,j>0} is such a language
An ambiguous grammar is a grammar for a language where at least one
string in the language has two parse trees. This is equivalent to
saying some string has more than one leftmost derivation or more
than one rightmost derivation.
Similar to Quiz 1
Covers Chapters 3 and 4 of book
Push Down Automata, PDA, are a way to represent the language class called
Context Free Languages, CFL, covered above. By themselves PDA's are not
very important but the hierarchy of Finite State Machines with
corresponding Regular Languages, PDA's with corresponding CFL's and
Turing Machines with corresponding Recursively Enumerable Sets (Languages),
is an important concept.
The definition of a Push Down Automata is:
M = (Q, Sigma, Gamma, delta, q0, Z0, F) where
Q = a finite set of states including q0
Sigma = a finite alphabet of input symbols (on the input tape)
Gamma = a finite set of push down stack symbols including Z0
delta = a group of nondeterministic transitions mapping
Q x (Sigma union {epsilon}) x Gamma to finite sets of Q x Gamma star
q0 = the initial state, an element of Q, possibly the only state
Z0 = the initial stack contents, an element of gamma, possibly the only
stack symbol
F = the set of final, accepting, states but may be empty for a PDA
"accepting on an empty stack"
Unlike finite automata, the delta is not presented in tabular form.
The table would be too wide. Delta is a list of, nondeterministic,
transitions of the form:
delta(q,a,A) = { (qi,gammai), (qj,gammaj), ...} where
q is the current state,
a is the input tape symbol being read, an element of Sigma union {epsilon}
A is the top of the stack being read,
The ordered pairs (q sub i, gamma sub i) are respectively the next state
and the string of symbols to be written onto the stack. The machine
is nondeterministic, meaning that all the pairs are executed causing
a branching tree of PDA configurations. Just like the branching tree
for nondeterministic finite automata except additional copies of the
pushdown stack are also created at each branch.
The operation of the PDA is to begin in state q0, read the symbol on the
input tape or read epsilon. If a symbol is read, the read head moves
to the right and can never reverse to read that symbol again.
The top of the stack is read by popping off the symbol.
Now, having a state, an input symbol and a stack symbol a delta transition
is performed. If there is no delta transition defined with these three
values the machine halts. If there is a delta transition with the (q,a,A)
then all pairs of (state,gamma) are performed. The gamma represents a
sequence of push down stack symbols and are pushed right to left onto
the stack. If gamma is epsilon, no symbols are pushed onto the stack. Then
the machine goes to the next state, q.
When the machine halts a decision is made to accept or reject th input.
If the last, rightmost, input symbol has not been read then reject.
If the machine is in a final state accept.
If the set of final states is empty, Phi, and the only symbol on the stack
is Z0, then accept. (This is the "accept on empty stack" case)
Now, using pictures we show the machines for FSM, PDA and TM
+-------------------------+----------------- DFA, NFA, NFA epsilon
| input string | accepts Regular Languages
+-------------------------+-----------------
^ read, move right
|
| +-----+
| | |--> accept
+--+ FSM | M = ( Q, Sigma, delta, q0, F)
| |--> reject
+-----+
+-------------------------+----------------- Push Down Automata
| input string |Z0 stack accepts Context Free Languages
+-------------------------+-----------------
^ read, move right ^ read and write (push and pop)
| |
+-----------------------+
| +-----+
| | |--> accept
+--+ FSM | M = ( Q, Sigma, Gamma, delta, q0, Z0, F)
| |--> reject
+-----+
+-------------------------+----------------- Turing Machine
| input string |BBBBBBBB ... accepts Recursively Enumerable
+-------------------------+----------------- Languages
^ read and write, move left and right
|
| +-----+
| | |--> accept
+--+ FSM | M = ( Q, Sigma, Gamma, delta, q0, B, F)
| |--> reject
+-----+
An example of a language that requires the PDA to be a NPDA,
Nondeterministic Push Down Automata,
is L = { w wr | w in Sigma and wr is w written backwards }
Given a Context Free Grammar, CFG, in Greibach Normal Form, A -> aB1B2B3...
Construct a PDA machine that accepts the same language as that grammar.
We are given G = ( V, T, P, S ) and must now construct
M = ( Q, Sigma, Gamma, delta, q0, Z0, F)
Q = {q} the one and only state!
Sigma = T
Gamma = V
delta is shown below
q0 = q
Z0 = S
F = Phi PDA will "accept on empty stack"
Now, for each production in P (individual production, no vertical bars)
A -> a gamma constructs
| | |
| | +-------------+
| | |
+-----------+ | gamma is a possibly empty, sequence of
| | | symbols from Gamma
+---+ | |
| | |
V V V
delta(q, a, A) = {(q, gamma), more may come from other productions}
If gamma is empty, use epsilon as in (q, epsilon)
Finished!
Given a NPDA M = ( Q, Sigma, Gamma, delta, q0, Z0, Phi) and
Sigma union Gamma = Phi,
Construct a CFG G = ( V, T, P, S )
Set T = Sigma
S = S
V = { S } union { [q,A,p] | q and p in Q and A in Gamma }
This can be a big set! q is every state with A every Gamma with
p every state. The cardinality of V, |V|=|Q|x|Sigma|x|Q|
Note that the symbology [q,A,p] is just a variable name.
Construct the productions in two stages, the S -> , then the [q,A,p] ->
S -> [q0,A,qi] for every qi in Q (including q0) |Q| of these productions
[q,A,qm+1] -> a[q1,B1,q2][q2,B2,q3][q3,B3,q4]...[qm,Bm,qm+1] is created
for each q, q1, q2, q3, q4, ..., qm+1 in Q
for each a in Sigma union {epsilon}
for each A,B1,B2,B3,...,Bm in Gamma
such that there is a delta of the form
delta(q,a,A) = { ...,(q1,B1B2B3...Bm), ...}
Note degenerate cases delta(q,a,A)={(q1,epsilon)} makes [q,A,q1] -> a
delta(q,epsilon,A)={(q1,epsilon)} makes [q,A,q1] -> epsilon
Pictorially, given delta(q0,a,A)= (q1,B1B2) generate the set
| | | | | | for q2 being every state,
+-------------+ | | | | | while qm+1 is every state
| +---------------+ | | |
| | | | | |
| | +--+ | | |
| | | +-------+ | |
| | | | +-------+ |
| | | | | |
V V V V V V
[q0,A,qm+1] -> a[q1,B1,q2][q2,B2,qm+1]
| | ^ ^
| | | |
| +---+ |
+--------------------------+
The book suggests to follow the chain of states starting with the right
sides of the S -> productions, then the new right sides of the [q,a,p] ->
productions. The correct grammar is built generating all productions.
Then the "simplification" can be applied to eliminate useless variables,
eliminate nullable variables, eliminate unit productions, convert to
Chomsky Normal Form, convert to Greibach Normal Form.
WOW! Now we have the Greibach Normal Form of a NPDA with any number of
states and we can convert this to a NPDA with just one state by the
construction in the previous lecture.
The important concept is that the constructions CFG to NPDA and NPDA to CFG
provably keep the same language being accepted. Well, to be technical,
The language generated by the CFG is exactly the language accepted by
the NPDA. Fixing up any technical details like renaming Gamma symbols
if Gamma union Sigma not empty and accepting or rejecting the null string
appropriately.
Use the "simplification" steps to get to a Chomsky Normal Form.
Use the algorithm on P140, Figure 6.8
The Pumping Lemma is generally used to prove a language is not context free.
If a PDA machine can be constructed to exactly accept
a language, then the language is a Context Free Language.
If a Context Free Grammar can be constructed to exactly generate the
strings in a language, then the language is Context Free.
To prove a language is not context free requires a specific definition of
the language and the use of the Pumping Lemma for Context Free Languages.
A note about proofs using the Pumping Lemma:
Given: Formal statements A and B.
A implies B.
If you can prove B is false, then you have proved A is false.
For the Pumping Lemma, the statement "A" is "L is a Context Free Language",
The statement "B" is a statement from the Predicate Calculus.
(This is a plain text file that uses words for the upside down A that
reads 'for all' and the backwards E that reads 'there exists')
Formal statement of the Pumping Lemma:
L is a Context Free Language implies
(there exists n)(for all z)[z in L and |z|>=n implies
{(there exists u,v,w,x,y)(z = uvwxy and |vwx|<=n and |vx|>1 and
i i
(for all i>=0)(uv wx y is in L) )}]
The two commonest ways to use the Pumping Lemma to prove a language
is NOT context free are:
a) show that there is no possible n for the (there exists n),
this is usually accomplished by showing a contradiction such
as (n+1)(n+1) < n*n+n
b) show there is no way to partition some z into u,v,w,x,y such that
i i
uv wx y is in L, typically for a value i=0 or i=2.
Be sure to cover all cases by argument or enumerating cases.
[This give a contradiction to the (for all z) clause.]
Some Context free languages and corresponding grammars:
i i
L={a b |i>=1} S->ab | aSb
2i 3i
L={a b | i>=1} S-> aabbb | aaSbbb [any pair of constants for 2,3]
i j i
L={a b c | i,j>=1} S->aBc | aSc B->b | bB
i i j
L={a b c | i,j>=1} S->DC D->ab | aDb C->c | cC
i i j j
L={a b a b | i,j>=1} S->CC C->ab | aCb
i i
L={ua wb y | i>=1 and u,w,y any fixed strings} S->uDy D->awb | aDb
R R
L={ww | w in Sigma star and w is w written backwards} S->xx | xSx
for all x in Sigma
Some languages that are NOT Context Free Languages
L={ww | w in Sigma star}
i i i
L={a b c | i>=1}
i j k
L={a b c | k > j > i >=1}
f(i) i
L={a b | i>=1} where f(i)=i**2 f(i) is the ith prime,
f(i) not bounded by a constant times i
i j i j
L={a b c d | i>=1}
Given two CFG's G1 = (V1, T1, P1, S1) for language L1(G1)
G2 = (V2, T2, P2, S2) for language L2(G2)
Rename variables until V1 intersect V2 is Phi.
We can easily get CFG's for the following languages:
L1 union L2 = L3(G3)
G3 = (V1 union V2 union {S3}, T1 union T2, P1+P2+P3, S3) S3 -> S1 | S2
L1 concatenated L2 = L4(G4)
G4 = (V1 union V2 union {S4}, T1 union T2, P1+P2+P4, S4) S4 -> S1S2
L1 star = L5(G5)
G5 = (V1 union V2 union {S5}, T1 union T2, P1+P2+P5, S5) S5 -> S5S1 | epsilon
Notice that L1 intersect L2 may not be a CFG.
i i j i j i
Example: L1={a b c | i,j>0} L2={a b c | i,j>0} are CFG's
i i i
but L1 intersect L2 = {a b c | i>0} which is not a CFG.
The complement of L1 may not be a CFG.
The intersection of a Context Free Language with a Regular Language
is a Context Free Language.
As a supplement, the following shows how to take a CFG and possibly
use 'yacc' or 'bison' to build a parser for the grammar.
The steps are to create a file xxx.y that includes the grammar,
and a file that is a main program that runs the parser.
An example grammar is coded in acfg.y
and a sample main program is coded in yymain.c
One possible set of commands to run the sample is:
bison acfg.y
gcc yymain.c acfg.tab.c
a.out
abaa
The output from this run shows the input being read and the rules
being applied:
read a
read b
read a
A -> ba
read a
read end of line \n converted to 0
S -> a
S -> aAS
accepted
M = ( Q, Sigma, Gamma, delta, q0, B, F)
Q = finite set of states including q0
Sigma = finite set of input symbols not including B
Gamma = finite set of tape symbols including Sigma and B
delta = transitions mapping Q x Gamma to Q x Gamma x {L,R}
q0 = initial state
B = blank tape symbol, initially on all tape not used for input
F = set of final states
+-------------------------+-----------------
| input string |BBBBB ... accepts Recursively Enumerable Languages
+-------------------------+-----------------
^ read and write, move left and right
|
| +-----+
| | |--> accept
+--+ FSM |
| |--> reject
+-----+
+-------------------------+-----------------
| input and output string |BBBBB ... computes partial recursive functions
+-------------------------+-----------------
^ read and write, move left and right
|
| +-----+
| | |
+--+ FSM |--> done (a delta [q,a]->[empty], but may never happen )
| |
+-----+
delta is a table or list of the form:
[qi, ai] -> [qj, aj, L] or [qi, ai] -> [qj, aj, R]
qi is the present state
ai is the symbol under the read/write head
qj is the next state
aj is written to the tape at the present position
L is move the read/write head left one position after the write
R is move the read/write head right one position after the write
It is generally a pain to "program" a Turing machine. You have to
convert the algorithm into the list of delta transitions. The fallback
is to describe in English the steps that should be performed. The
amount of detail needed depends on the reader of the algorithm
accepting that there is an obvious way for the Turing machine to
perform your steps.
There are a lot of possible Turing machines and a useful technique
is to code Turing machines as binary integers. A trivial coding is
to use the 8 bit ASCII for each character in the written description
of a Turing machine concatenated into one long bit stream.
Having encoded a specific Turing machine as a binary integer, we
can talk about TMi as the Turing machine encoded as the number "i".
It turns out that the set of all Turing machines is countable and
enumerable.
Now we can construct a Universal Turing Machine, UTM, that takes
an encoded Turing machine on its input tape followed by normal
Turing machine input data on that same input tape. The Universal Turing
Machine first reads the description of the Turing machine on the
input tape and uses this description to simulate the Turing machines
actions on the following input data. Of course a UTM is a TM and can
thus be encoded as a binary integer, so a UTM can read a UTM from
the input tape, read a TM from the input tape, then read the input
data from the input tape and proceed to simulate the UTM that is
simulating the TM. Etc. Etc. Etc.
In the next lecture we will make use of the fact that a UTM can be
represented as an integer and can thus also be the input data on
the input tape.
The "Halting Problem" is a very strong, provably correct, statement
that no one will ever be able to write a computer program or design
a Turing machine that can determine if a arbitrary program will
halt (stop, exit) for a given input.
This is NOT saying that some programs or some Turing machines can not
be analyzed to determine that they, for example, always halt.
The Halting Problem says that no computer program or Turing machine
can determine if ALL computer programs or Turing machines will halt
or not halt on ALL inputs. To prove the Halting Problem is
unsolvable we will construct one program and one input for which
there is no computer program or Turing machine.
We will use very powerful mathematical concepts and do the proofs
for both a computer program and a Turing machine. The mathematical
concepts we need are:
Proof by contradiction. Assume a statement is true, show that the
assumption leads to a contradiction. Thus the statement is proven false.
Self referral. Have a computer program or a Turing machine operate
on itself, well, a copy of itself, as input data. Specifically we
will use diagonalization, taking the enumeration of Turing machines
and using TMi as input to TMi.
Logical negation. Take a black box that accepts input and outputs
true or false, put that black box in a bigger black box that
switches the output so it is false or true respectively.
The simplest demonstration of how to use these mathematical concepts
to get an unsolvable problem is to write on the front and back of
a piece of paper "The statement on the back of this paper is false."
Starting on side 1, you could choose "True" and thus deduce side 2
is "False". But staring on side 2, which is exactly the same as
side 1, you get that side 2 is "True" and side 1 is "False."
Since side 1, and side 2, can be both "True" and "False" there
is a contradiction. The problem of determining if sides 1 and 2 are
"True" of "False" is unsolvable.
The Halting Problem for a programming language. We will use the "C"
programming language, yet any language will work.
Assumption: There exists a way to write a function named Halts such that:
int Halts(char * P, char * I)
{
/* code that reads the source code for a "C" program, P,
determines that P is a legal program, then determines if P
eventually halts (or exits) when P reads the input string I,
and finally sets a variable "halt" to 1 if P halts on input I,
else sets "halt" to 0 */
return halt;
}
Construct a program called Diagonal.c as follows:
int main()
{
char I[100000000]; /* make as big as you want or use malloc */
read_a_C_program_into( I );
if ( Halts(I,I) ) { while(1){} } /* loop forever, means does not halt */
else return 1;
}
Compile and link Diagonal.c into the executable program Diagonal.
Now execute
Diagonal < Diagonal.c
Consider two mutually exclusive cases:
Case 1: Halts(I,I) returns a value 1.
This means, by the definition of Halts, that Diagonal.c halts
when given the input Diagonal.c.
BUT! we are running Diagonal.c (having been compiled and linked)
and so we see that Halts(I,I) returns a value 1 causes the "if"
statement to be true and the "while(1){}" statement to be executed,
which never halts, thus our executing Diagonal.c does NOT halt.
This is a contradiction because this case says that Diagonal.c
does halt when given input Diagonal.c.
Well, try the other case.
Case 2: Halts(I,I) returns a value 0.
This means, by the definition of halts, that Diagonal.c does NOT
halt when given the input Diagonal.c.
BUT! we are running Diagonal.c (having been compiled and linked)
and so we see that Halts(I,I) returns a value 0 causes the "else"
to be executed and the main function halts (stops, exits).
This is a contradiction because this case says that Diagonal.c
does NOT halt when given input Diagonal.c.
There are no other cases, Halts can only return 1 or 0.
Thus what must be wrong is our assumption "there exists a way
to write a function named Halts..."
The Halting Problem for Turing machines.
Assumption: There exists a Turing machine, TMh, such that:
When the input tape contains the encoding of a Turing machine, TMj followed
by input data k, TMh accepts if TMj halts with input k and TMh rejects
if TMj is not a Turing machine or TMj does not halt with input k.
Note that TMh always halts and either accepts or rejects.
Pictorially TMh is:
+----------------------------
| encoded TMj B k BBBBB ...
+----------------------------
^ read and write, move left and right
|
| +-----+
| | |--> accept
+--+ FSM | always halts
| |--> reject
+-----+
We now use the machine TMh to construct another Turing machine TMi.
We take the Finite State Machine, FSM, from TMh and
1) make none of its states be final states
2) add a non final state ql that on all inputs goes to ql
3) add a final state qf that is the accepting state
Pictorially TMi is:
+-------------------------------------------
| encoded TMj B k BBBBB ...
+-------------------------------------------
^ read and write, move left and right
|
| +----------------------------------+
| | __ |
| | / \ 0,1 |
| | +-| ql |--+ |
| | +-----+ | \___/ | |
| | | |--> accept-+ ^ | |
+--+-+ FSM | |_____| | may not halt
| | |--> reject-+ _ |
| +-----+ | // \\ |
| +-||qf ||------|--> accept
| \\_// |
+----------------------------------+
We now have Turing machine TMi operate on a tape that has TMi as
the input machine and TMi as the input data.
+-------------------------------------------
| encoded TMi B encoded TMi BBBBB ...
+-------------------------------------------
^ read and write, move left and right
|
| +----------------------------------+
| | __ |
| | / \ 0,1 |
| | +-| ql |--+ |
| | +-----+ | \___/ | |
| | | |--> accept-+ ^ | |
+--+-+ FSM | |_____| | may not halt
| | |--> reject-+ _ |
| +-----+ | // \\ |
| +-||qf ||------|--> accept
| \\_// |
+----------------------------------+
Consider two mutually exclusive cases:
Case 1: The FSM accepts thus TMi enters the state ql.
This means, by the definition of TMh that TMi halts with input TMi.
BUT! we are running TMi on input TMi with input TMi
and so we see that the FSM accepting causes TMi to loop forever
thus NOT halting.
This is a contradiction because this case says that TMi
does halt when given input TMi with input TMi.
Well, try the other case.
Case 2: The FSM rejects thus TMi enters the state qf.
This means, by the definition of TMh that TMi does NOT halt with
input TMi.
BUT! we are running TMi on input TMi with input TMi
and so we see that the FSM rejecting cause TMi to accept and halt.
This is a contradiction because this case says that TMi
does NOT halt when given input TMi with input TMi.
There are no other cases, FSM either accepts or rejects.
Thus what must be wrong is our assumption "there exists a
Turing machine, TMh, such that..."
QED.
Thus we have proved that no Turing machine TMh can ever be created
that can be given the encoding of any Turing machine, TMj, and any input, k,
and always determine if TMj halts on input k.
This is a mathematically unprovable belief that a reasonable intuitive
definition of "computable" is equivalent to the list provably equivalent
formal models of computation:
Turing machines
Lambda Calculus
Post Formal Systems
Partial Recursive Functions
Unrestricted Grammars
Recursively Enumerable Languages (decision problems)
and intuitively what is computable by a computer program written in any
reasonable programming language.
Mostly review
On paper, graded exams in box outside office door, ECS 219.
Last updated 12/7/98