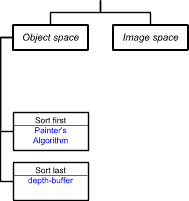
Calculating Intersections
: Polygons
Define ray parametrically:
- x = x0 + t . [delta]x
- y = y0 + t . [delta]y
- z = z0 + t . [delta]z
(1) What is intersection of ray and plane containing polygon?
- Plane : Ax + By + Cz + D = 0
Substituting for x, y, z:
- A(x0 + t . [delta]x) + B(y0 + t . [delta]y) + C(z0 + t . [delta]z) + D = 0
- t(A . [delta]x + B . [delta]y + C . [delta]z) + (Ax0 + By0 + Cz0 + D) = 0
- t = - (Ax0 + By0 + Cz0 + D) / (A . [delta]x + B . [delta]y + C . [delta]z)
(2) Does ray/plane intersection point lie in polygon?
- Substitute into line equations for polygon edges
does point lie inside all edges? <= convex!
- Count edge crossings of ray from point to infinity
- odd : inside
- even : outside
- Winding number testing
Determining if Point is in Polygon
|
Determining if Point is in Polygon
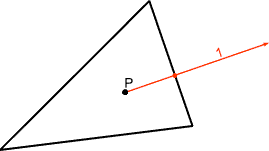
|
Determining if Point is in Polygon
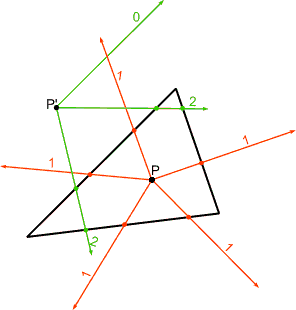
- 1 corssing => inside
- 0,2 corssing => outside
|
Determining if Point is in Polygon
|
Determining if Point is in Polygon
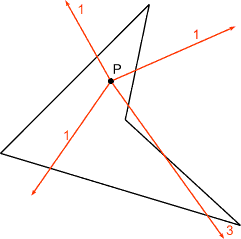
- odd number of corssings => inside
|
Determining if Point is in Polygon
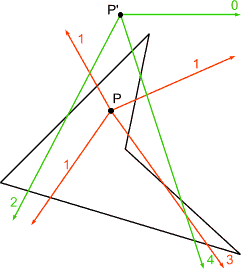
- odd number of corssings => inside
- even number of corssings => outside
|
Determining if Point is in Polygon
|
Determining if Point is in Polygon
|
Determining if Point is in Polygon
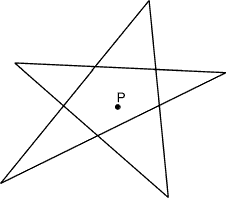
Self intersecting polygon
Odd even rule
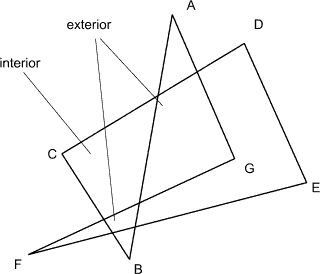
Count each crossing as one
|
Determining if Point is in Polygon
Self intersecting polygon
Odd even rule
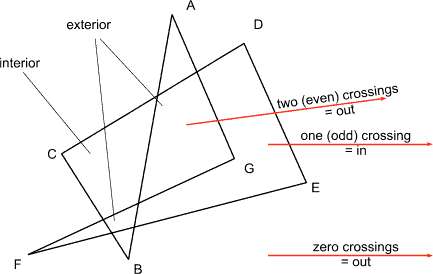
Count each crossing as one
|
Determining if Point is in Polygon
Self intersecting polygon
Odd even rule
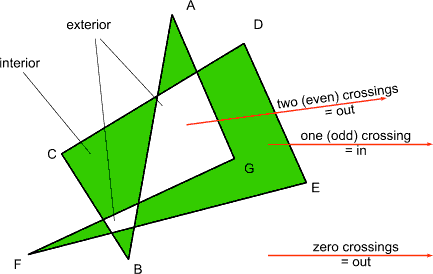
Count each crossing as one
|
Determining if Point is in Polygon
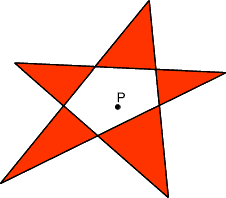
Self intersecting polygon
Nonzero winding number rule
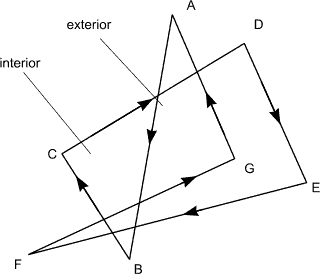
|
Determining if Point is in Polygon
Self intersecting polygon
Nonzero winding number rule
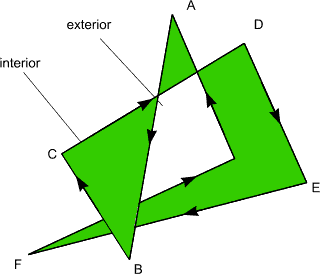
Count number of times border wraps point
- + clockwise
- - counterclockwise
NC = 0 : outside
NC != 0 : inside
|
Ray-Tracing: Characteristics
Good:
- Simple to implement
- Minimal memory required
- Easy to extend
- Reflaction
- Refraction
- Other geometric primitives
|
Ray-Tracing: Characteristics
Good:
- Simple to implement
- Minimal memory required
- Easy to extend
- Reflaction
- Refraction
- Other geometric primitives
Bad
- Aliasing
- Computationally intensive
- Intersections expensive (75 - 95% of rendering time)
- Lots of rays
|
Taxonomy of Visibility Algorithms
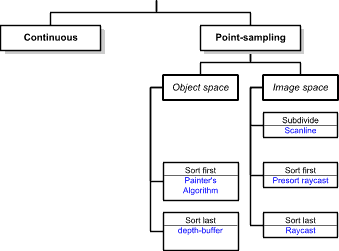
|
Taxonomy of Visibility Algorithms
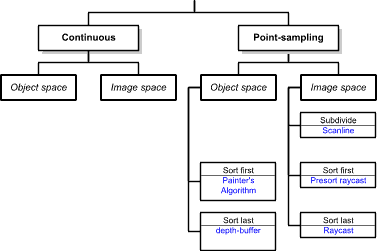
|
Taxonomy of Visibility Algorithms
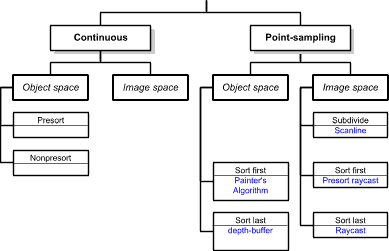
|
Taxonomy of Visibility Algorithms
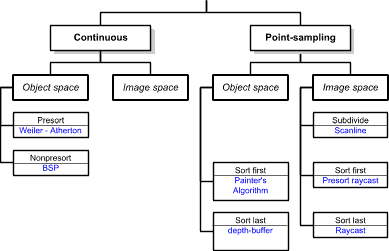
|
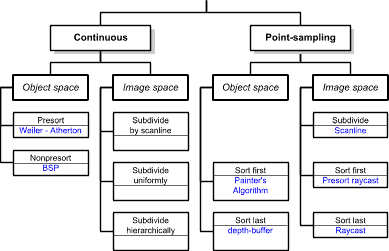
Taxonomy of Visibility Algorithms
|
Taxonomy of Visibility Algorithms
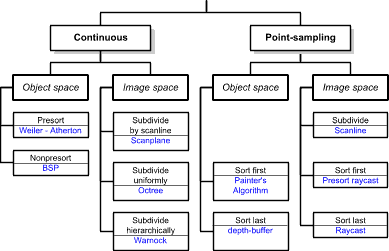
|
BSP Tree Method : Building the Tree
BSPTree MakeBSP ( Polygon list )
{
if ( list is empty )
return null
else {
root = some polygon ; remove it from the list
backlist = frontlist = null
for ( each remaining polygon in the list ) {
if ( p in front of root ) {
add to list ( p, front list )
}
else if ( p in back of root ) {
add to list ( p, back list )
}
else {
split polygon ( p, root, frontpart, backpart )
add to list ( frontpart, front list )
add to list ( backpart, back list )
}
}
return ( combine tree ( MakeBSP ( front list ), root,
MakeBSP ( back list ) ) )
}
}
|
Building a BSP Tree
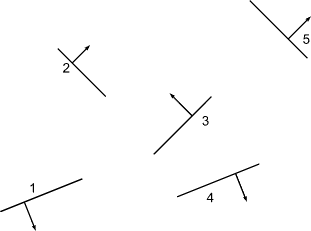
|
Building a BSP Tree
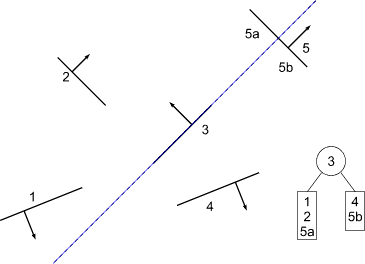
Use 3 as root, split on its plane.
Polygon 5 split into 5a and 5b
|
Building a BSP Tree
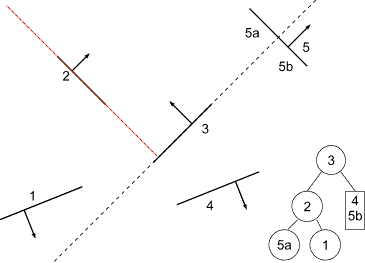
Split left subtree at 2
|
Building a BSP Tree
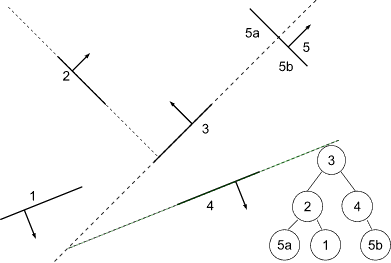
Split right subtree at 4
|
Building a BSP Tree
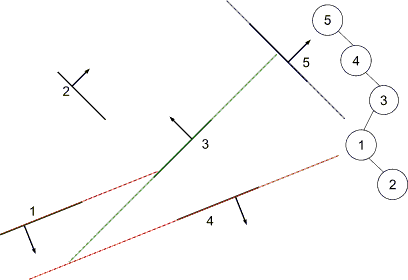
Tree if splits are made at 5, 4, 3, 1
|
BSP Tree Method : Displaying the Tree
DisplayBSP ( tree )
{
if ( tree not empty ) {
if ( viewer in front of root ) {
DisplayBSP ( tree -> back )
DisplayPolygon ( tree -> root )
DisplayBSP ( tree -> front )
}
else {
DisplayBSP ( tree -> front )
DisplayPolygon ( tree -> root )
DisplayBSP ( tree -> back )
}
}
}
|
BSP Tree Display
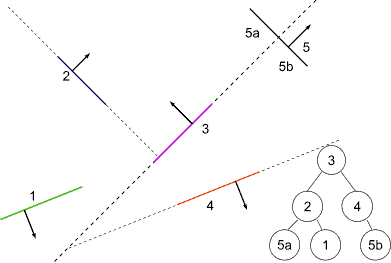
|
BSP Tree Display
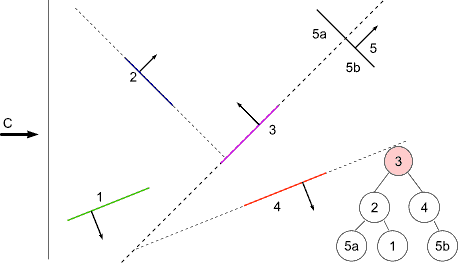
For view point at C
at 3 : viewpoint on front -> display back first
|
BSP Tree Display
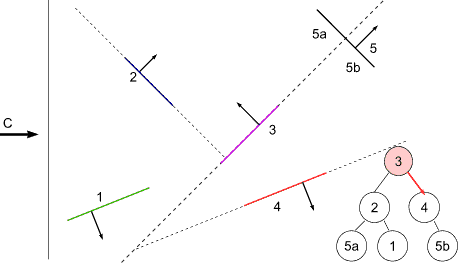
For view point at C
at 3 : viewpoint on front -> display back first
at 4 : viewpoint on back -> display front first
|
BSP Tree Display
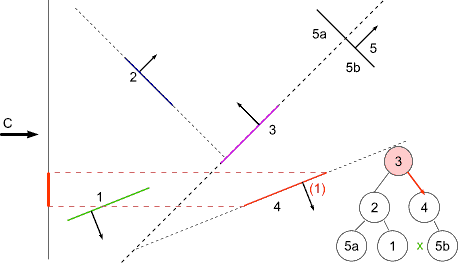
For view point at C
at 3 : viewpoint on front -> display back first
at 4 : viewpoint on back -> display front first (none)
display self
|
BSP Tree Display
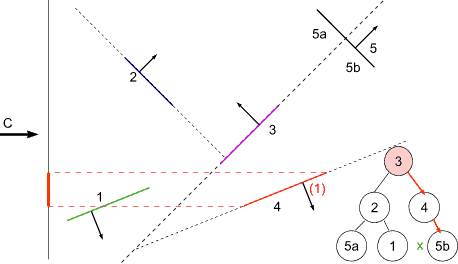
For view point at C
at 3 : viewpoint on front -> display back first
at 4 : viewpoint on back -> display front first (none)
display self
display back
|
BSP Tree Display
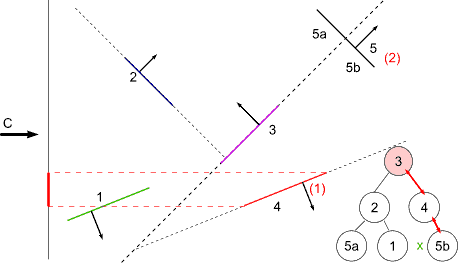
For view point at C
at 3 : viewpoint on front -> display back first
at 4 : viewpoint on back -> display front first (none)
display self
display back
at 5b : viewpoint on back -> display front (none)
display self
display back (none)
|
BSP Tree Display
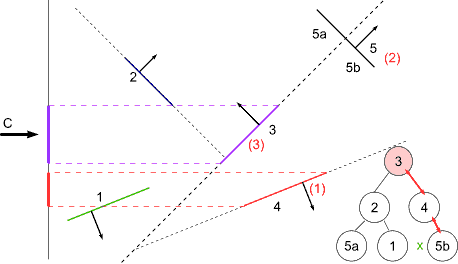
For view point at C
at 3 : viewpoint on front -> display back first
at 4 : viewpoint on back -> display front first (none)
display self
display back
at 5b : viewpoint on back -> display front
display self
display back (none)
display self
|
BSP Tree Display

For view point at C
at 3 : viewpoint on front -> display back first
at 4 : viewpoint on back -> display front first (none)
display self
display back
at 5b : viewpoint on back -> display front (none)
display self
display back (none)
display self
display front
|
BSP Tree Display
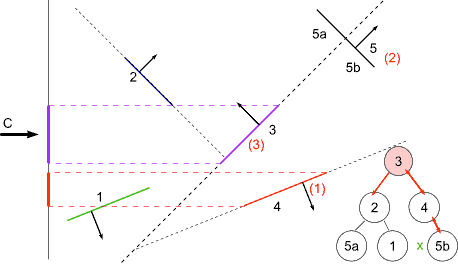
For view point at C
at 3 : viewpoint on front -> display back first
at 4 : viewpoint on back -> display front first (none)
display self
display back
at 5b : viewpoint on back -> display front (none)
display self
display back (none)
display self
display front
at 2 : viewpoint on back -> display front first
|
BSP Tree Display
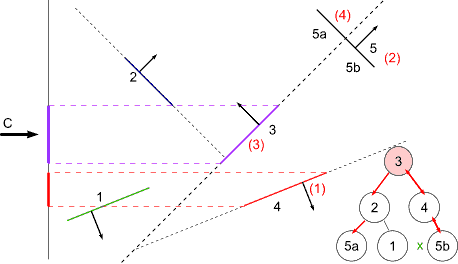
For view point at C
at 3 : viewpoint on front -> display back first
at 4 : viewpoint on back -> display front first (none)
display self
display back
at 5b : viewpoint on back -> display front (none)
display self
display back (none)
display self
display front
at 2 : viewpoint on back -> display front first
at 5a : viewpoint on back -> display front (none)
display self
display back (none)
|
BSP Tree Display
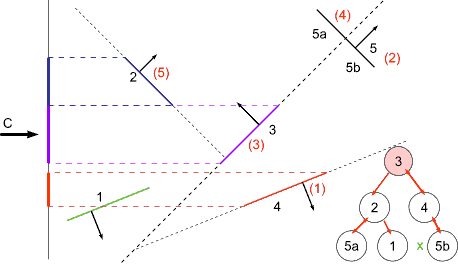
For view point at C
at 3 : viewpoint on front -> display back first
at 4 : viewpoint on back -> display front first (none)
display self
display back
at 5b : viewpoint on back -> display front (none)
display self
display back (none)
display self
display front
at 2 : viewpoint on back -> display front first
at 5a : viewpoint on back -> display front (none)
display self
display back (none)
display self
|
BSP Tree Display
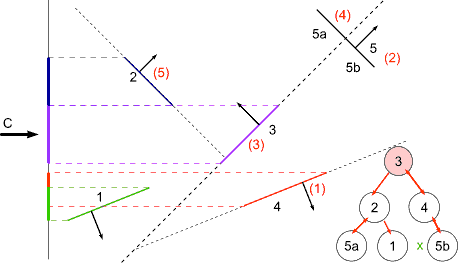
For view point at C
at 3 : viewpoint on front -> display back first
at 4 : viewpoint on back -> display front first (none)
display self
display back
at 5b : viewpoint on back -> display front (none)
display self
display back (none)
display self
display front
at 2 : viewpoint on back -> display front first
at 5a : viewpoint on back -> display front (none)
display self
display back (none)
display self
at 1 : viewpoint on back -> display front (none)
display self
display back (none)
|
![[prev]](common/prev.gif) ![[next]](common/next.gif)
|
![[prev]](common/prev.gif)
![[next]](common/next.gif)
![[prev]](common/prev.gif)
![[next]](common/next.gif)