 |
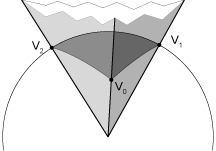
V0×V1 • P ≥ 0 V1×V2 • P ≥ 0 V2×V0 • P ≥ 0 |
Last updates:
Fri Sep 29 14:34 EDT 2006
For this assignment, you will be modifying your last assignment to drive a vehicle around on your random planetoid. You will replace the former parallel projection with a perspective projection from the point of view of a person sitting in a vehicle approximately 1 meter above the ground. You will also replace the mouse motion handler with a new one that maps horizontal mouse motion to looking left and right and vertical mouse motion to speeding up and slowing down your vehicle speed. The view should tip to align with the landscape as you move. You are free to start at any location you choose on the planetoid (so you can assume you know the starting triangle if that makes things easier for you), but you should not constrain the user's ability to drive around the planetoid in any way.
Include a mode with a third-person perspective viewpoint slightly above and behind your vehicle. When in this mode, you should render a simple model of your vehicle on the landscape. Allow a user to toggle between this mode and the vehicle point of view mode with the 'v' key.
Write up a short proposal for how your project could be extended into a submission for the Hidden Agenda contest (www.hiddenagenda.com). This contest is for games designed by college students to be both fun and educational for middle-school students. If you try for the extra credit, be sure to read all of the contest rules. Submit your proposal as a a text file named game.txt in your assignment directory. You should specifically tell us how the game will be played, and which of the approved subjects your game would teach and how. Unlike the assignment, the contest allows the use of specific additional game development tools, as well as a team of up to eight. How would you extend and partition your project to use these additional resources?
To figure out the position of your vehicle and the up-vector for the view, you will first need to figure out which triangle you are in. The basic operation you will need is a point in spherical triangle test. Whatever radius is used for the triangle vertices, the triangle is always guaranteed to cap a triangluar wedge from the center of the sphere. You can tell if a point is in this wedge, and therefore in the triangle, by evaluating the plane equations for the sides of the wedge. Each side plane is defined by the origin and two of the triangle vertices. If your location passes all three plane equations, you know you are inside that triangle.
|
There are two alternate ways to use this test to find your location. The first is to update your 'current triangle' incrementally whenever one of the plane equations has the wrong sign. Since it is possible to move across multiple triangles in a frame (especially if you leave a triangle at or one of its vertices), you should keep updating until you have found the final triangle containing the new position. The second method is to first find the top-level octahedron triangle containing the viewpoint, then recursively apply the triangle test to find which of the four subtriangles contain the viewpoint until you get to the smallest triangles for the current level of subdivision.
Once you know which triangle your vehicle is sitting on, you will need to construct barycentric coordinates for your position in the triangle (see section 2.11 in the book), and interpolate the per-vertex positions to find your location, and the per-vertex normals to find your up vector. Perspective projection should be applied in the OpenGL projection matrix stack (glMatrixMode(GL_PROJECTION)), while viewing transformations should be applied in the OpenGL model/view matrix stack (glMatrixMode(GL_MODELVIEW)). It is probably easiest to move the view matrix setup into your draw function and just update state in your motion function.
You make continuous motion by making changes each frame then redrawing. Normally, GLUT only calls your draw function if something it knows about changes. However, if you call glutPostRedisplay() inside your draw function, it will cause GLUT to call your draw function again for a new frame as soon as the current frame is complete (the mouse motion handler already does this to force a redraw when the mouse moves). To animate continuous motion, decide your speed in meters per second, figure out how much time has elapsed using gettimeofday(), then move your viewpoint an appropriate distance forward and adjust the position and view to remain on the surface.
Plan ahead! Know how you're going to find the position and view vector. Once you have a plan, implement in stages that each produce a visible result. While it is not part of the assigned project, it may also be useful to set up extra keys to show debugging results. For example, a key that switches from the perspective view to an 'assignment 2' view with the vehicle triangle marked in a different color or vehicle postion marked by a glutSolidSphere could be helpful if you are having trouble debugging your position code.
If your assignment 2 did not work, you can get a working sample version from me after you have turned in your final version of assignment 2. However, I would encourage you to start from your own assignment 2 code if at all possible. Problems with your assignment 2 will not count against your assignment 3 grade, but you should at least have some landscape height and smooth per-vertex normals.
You may find the following OpenGL calls helpful to complete the assignment:
As usual, turn in this assignment electronically by checking it into your Assn3 CVS directory by 11:59 PM on the day of the deadline. We will use a dated checkout for grading, so you will be graded on whatever has been checked in as of 11:59 PM. Submit a readme.txt file telling us about your assignment. What (if any) help did you receive from books, web sites or people other than the instructor and TA? How did you choose to find your triangle location? What else notable about your program? Include your modified Makefile, any C/C++ files, and any other auxiliary files we might need so we can just run 'make' in on a linux.gl machine to build your project. Be sure to comment your code! You will not be graded on the presence or quality of your comments, but we will look at your code and anything that helps us understand what you did (or were trying to do) can only help. In any case, your programs are expected to be robust and easy to understand.
As a reminder, gl machines include all of the OpenGL man pages (you don't have to be sitting at one, you can just 'ssh gl.umbc.edu'). Just try 'man glFrustum', etc. to find out more about any function used in the assignment that sparks your curiosity. Also, the OpenGL 1.1 Programmers Guide (the "OpenGL red book") is available online, and is a good reference