CMSC 435/634: Introduction to Computer Graphics
Assignment 4
Modeled Scene
Due October 21, 2002
Now with color coded updates new..old.
Last update: Thu Oct 10 15:13:26 EDT 2002
The Assignment
For this assignment, you will be creating a simple procedurally modeled
scene, with a mountainous fractal island on a blue sea. The sea can be
created from a single blue polygon. The island will be created by
recursively subdividing two triangles, using a slight modification of
the fractal mountain construction method described in class. The island
should be lit by one OpenGL distant light (simulating the sun or moon)
and one ambient light (simulating light from atmospheric scattering).
For lighting to work, you will need to compute surface normals for each
triangle you draw. One way to get this is to take the cross product of
two of the edges. Compute all of the geometry in advance, when your
program starts up. You should only be rendering and processing user
interaction in the rendering loop. Your program should take two numeric
command line arguments. One for the number of subdivisions to perform
and one for the random number seed. Especially if you do the extra
credit, you may want to provide some suggested seed values.
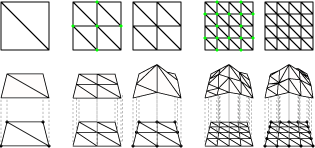
As a reminder, to construct a fractal mountain, you start with a
triangle or set of triangles. At each step, you split each existing
triangle into four. This is shown in the figure
below with the new vertices marked with green dots. A simple
splitting places the new vertices at the midpoints of the edges (as shown on the left of each pair in the figure),
you will then perturb these new vertex locations vertically by some
random amount (as shown on the right in each pair
in the figure). At each step, reduce the scale of your random
perturbation by 1/2. This sequence gives the characteristic fractal
self-similarity: at half the scale, you have half the noise amplitude.
Sometimes when modeling natural processes (as we are here), this called
1/f noise because the noise amplitude is proportional to 1/f for noise
frequency f (controlled in this case by the geometric splitting).
The base triangles of your island should be below sea level. The
shape of the shoreline will be determined by the contour where the sea
polygon intersects the island. To make sure that the edges of your
island don't pop up above the level of the sea, you should modify the
algorithm to clamp all edge vertices to make sure they don't protrude
above sea level. In this diagram, the points marked with black dots can be allowed to move, but not
above the level of the sea.
Once again, I have provided some OpenGL code to get you started.
This code, in ~olano/public/cs435/assn4. It is similar to the sample
code from assignments 2 and 3, but adds an example of the use of OpenGL
lighting.
Strategy
There are several ways you could program the procedural mountain. Those
details are up to you. I do suggest breaking it down into simple parts
that produce visual results as a useful graphics development and
debugging technique.
Extra credit
For the base project, your island could be solid green or brown or even
grey. For up to 10 extra credit points, make the island scene look as
realistic as you can. A good place to start is the altitude-based
coloring mentioned in class, but you can do whatever you want. The extra
credit will be graded based on realism and creativity.
What to turn in
Turn in this assignment electronically as 'cs435 Proj4' using the
submit mechanism:
submit cs435 Proj4 [files...]
If submitting after the due date, submit as Proj4late. In either case,
you should all files that you created or modified. We should be
able to copy the submitted files into a clean copy of assn4 and be able
to build and run your project. The only way we'll be able to grade this
time is to build and run your project. Please make sure it will run on
linux.gl.umbc.edu or irix.gl.umbc.edu (and let us know which to use). Be
sure to leave time to port if you develop on a system other than one of
these!
As always, we will be looking at your source code, so please try to
make it understandable and comment anything you want to make sure we
notice. 'This is what I'm doing' comments are more useful for my
understanding than comments like 'add x to y'. Additional
comments may help your grade in cases where your program does not
operate entirely correctly (since they can give me insight into what you
were trying to do). In any case, your programs are expected to be
robust and easy to understand.
References
For anyone looking for more information on OpenGL, the irix machines
include all of the OpenGL man pages (you don't have to be sitting at
one, you can just 'ssh irix.gl.umbc.edu'). Just try 'man
glVertex2f', etc. to find out more about any function used in the
assignment that sparks your curiosity. Also, the OpenGL
1.1 Programmers Guide (the "OpenGL red book") is available online.
This a good introduction to writing OpenGL programs.
Working at home
If you managed to work from home last time, you're in luck since this
project uses the same set of libraries. If not, the usual caveats apply:
If it comes down to a choice between the two, remember that your grade
is based on a working project, not a successfully installed GLUT
library. In the end, the project MUST run on linux.gl.umbc.edu or
irix.gl.umbc.edu. Be sure to test it before you submit!