CMSC 435/634 Fall 2002, Assignment 3

CMSC 435/634: Introduction to Computer Graphics

Assignment 3
Modeling (opt/grad)
Due October 4, 2002

Grading

This assignment is required for students taking 634. Students taking 435 who choose to do the assignment can earn a maximum of 30 points extra credit.

Background

Spline patches are a common modeling tool. Many modeling packages provide a flexible means to design objects out of a collection of patches, producing patch control points which must be used by a renderer to render. For this assignment, we will be that renderer.

Once again, I have provided some OpenGL code to get you started. This code, in ~olano/public/cs435/assn3, may look familiar as it is based on the polygons.c file I provided for Assignment 2. The sample code for this assignment adds the following features:

Enables OpenGL depth-buffer so we can draw solid objects
Adds mouse control for moving the model when you're on a fast computer
It's pre-split into multiple files. Most, if not all, of your code will go into drawpatch.c
The sample code has been tested to compile with both C and C++ compilers, making life a bit easier for the C++ crowd.
Saving of images was removed since variations in the ImageMagick library installation across campus caused many build problems last time. You're free to add image saving back in if you want, just copy the code and ImageMagick makefile changes from last time.

The Assignment

You will read patch control points for a set of bicubic patches from a file. You will subdivide into some number of smaller patches, with the degree of subdivision under keyboard control (Use '+' or '=' to increase the subdivision and '-' or '_' to decrease the subdivision). You'll then draw the subdivide patch mesh using four triangles per patch, with each triangle connecting two corner control points to a common center point. You should draw each triangle in a random color.

Patch file

The patch file will has the following format: Blank lines or lines starting with '#' should be ignored. Each remaining line will have four 3D control point coordinate (12 numbers). A full bicubic patch will have sixteen control point lines in the following order

 0  1  2  3
 4  5  6  7
 8  9 10 11
12 13 14 15

The sample patch file is for the Utah or Newell teapot, a classic test model in computer graphics.

Triangles

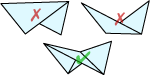We could use two triangles to connect the four corners of each patch for final drawing (and it is often done this way). However, since we are not basing our level of subdivision on either size or flatness, we will sometimes get strange folds on saddle shaped patches. By adding a vertex at patch coordinates (.5,.5) (which happens to be one corner from the next level of subdivision), we'll have a slightly better appearance for these patches.

Random colors

Completely random colors may include black or dark colors that will be difficult to see against the black window background. Avoid colors where red+green+blue < 0.25. Any method you use to limit the color selection is fine. Here are three suggestions:

discard colors that are out of range and pick again.
limit the range of the last color (pick red from 0 to 1, green from 0 to 1, blue from min(0,.25-red-green) to 1.
pick from a pre-defined or pre-generated list of acceptable colors (at least a couple hundred for variety)

What to turn in

Turn in this assignment electronically as 'cs435 Proj3' using the submit mechanism:

    submit cs435 Proj3 [files...]

If submitting after the due date, submit as Proj3late. In either case, you should all files that you created or modified. We should be able to copy the submitted files into a clean copy of assn3 and be able to build and run your project. The only way we'll be able to grade this time is to build and run your project. Please make sure it will run on linux.gl.umbc.edu or irix.gl.umbc.edu (and let us know which to use).

We will be looking at your source code, so please try to make it understandable and comment anything you want to make sure we notice. 'This is what I'm doing' comments are more useful for my understanding than comments like 'add x to y'As always, additional comments may help your grade in cases where your program does not operate entirely correctly (since they can give me insight into what you were trying to do). In any case, your programs are expected to be robust and easy to understand.

References

For anyone looking for more information on OpenGL, the irix machines include all of the OpenGL man pages (you don't have to be sitting at one, you can just 'ssh irix.gl.umbc.edu'). Just try 'man glVertex2f', etc. to find out more about any function used in the assignment that sparks your curiosity. Also, the OpenGL 1.1 Programmers Guide (the "OpenGL red book") is available online. This a good introduction to writing OpenGL programs.

Working at home

If you managed to work from home last time, you're in luck since this project uses the same set of libraries. If not, the usual caveats apply: If it comes down to a choice between the two, remember that your grade is based on a working project, not a successfully installed GLUT library. In the end, the project MUST run over ssh to either linux.gl.umbc.edu or irix.gl.umbc.edu. Be sure to test it before you submit.