CMSC 491A/691A
Procedural Texturing
Fall 2000
David S. Ebert
Computer Science and Electrical Engineering Department
University of Maryland, Baltimore County
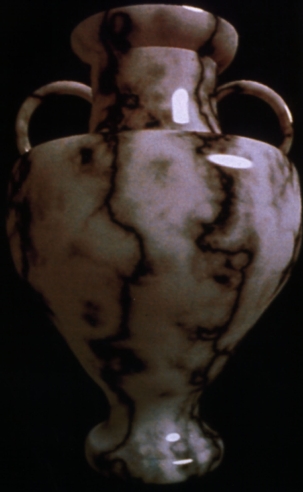
Marble Vase by Ken Perlin, 1985
Traditional Texture Mapping (Ed
Catmull 1974) :
Use of scanned in photograph or pre-computed
information to "wrap" around an object to simulate greater complexity.
Advantages:
Less complex models
Easy to acquire photos ??
Disadvantages:
Storage
Aliase prone
Photos already have illumination calculations done
Mapping complex
Example

Procedural Texturing (Gardner 1984, Peachey, Perlin 1985)

Procedural Techniques:
Definition
-
use of code segments or algorithms to generate object
description, attribute, motion, etc.
Advantages:
-
detail on demand
-
flexibility
-
data amplification
-
parametric control
-
2D Procedural Textures:
-
space savings
-
adaptability to geometry
-
more efficient ?? -- Sometimes
-
Example 2D Procedural Texture:
Sample_Procedure(x,y,color)
{
static
int first=1;
color.r=color.g=color.b=0;
if(first)
{ first=0;
for (i=0; i < 20; i++)
{
center[i].x = drand48()*10;
center[i].y = drand48()*10;
radius[i] = drand48*.5; radius[i] *=radius[i];
color[i].r = drand48(); color[i].g=drand48();
color[i].b=drand48();
}
}
for (i=0;
i < 20; i++)
{
dist_sq = (center[i].x-x)*(center[i].x-x) +
(center[i].y-y)*(center[i].y-y)
if (dist_sq < radius[i])
color=color[i];
break;
}
}
Solid Texturing
-
3D texture space
-
Mapping is now simple affine transformation
-
Can use 3D scanned images (CT, MR, ...)
-- excessive memory cost
-
Appeared in 1985 by Peachey, Perlin; (also in 1984
by Gardner)
-
Object Carving
Applying texture function is like carving away the defining
space


-
Natural for object made from solid material
Examples:


-
Solid Texturing Procedures (Toolbox)
-
Primitives
-
trigonometric functions
-
noise
-
turbulence
-
bombing
-
bias/gain
-
cellular functions
-
...
Trigonometric Functions
example:
-
sin(y) -- horizontal stripes
- color.r = color.g =color.b = sin(pnt.y);
- sin(pnt.x) = vertical stripes
-

-
tan -- Can be used for wood
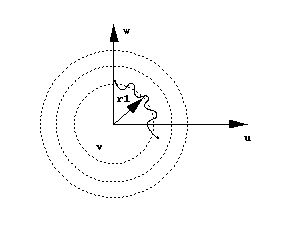
Vertical cylinder
- r1 = sqrt (u2 + w2
Add variation
- r2 = r1 + 2 sin(a*theta + v/b)
where
- theta = tan-1(u/w)
and v varies with height. Do mod on r2
to get cylinder colors. Could also do sin of r2, but
still too regular.
-
exponential -- More natural falloff than linear falloff
-
splines - smooth transitions, 2nd dreivative
continuity
-
power function
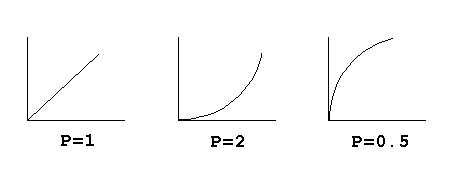
Stochastic Procedures
Noise

-
simulation of uncorrelated random noise
-
desired properties
-
statistical invariance under rotation
-
statistical invariance under translation
-
narrow bandpass limit in frequency to allows anti-aliasing
-
Perlin's Lattice Noise implementation
-
integer lattice w/ random values at each point
-
values not at lattice points are interpolated
-
replicate to fill 3 space
-
interpolation can be
-
Perlin's Gradient Noise
-
integer lattice w/ random unit vectors at each point
-
values not at lattice points are interpolated, using
gradients as spline coefficients
-
Less regularity artifacts
-
Example:

- J. P. Lewis gives better noise functions
- Peachey gives several implementation
-
- value noise
-
- gradient noise
-
- sparse convolution noise
-
- spectral synthesis (Fourier)
-
Scaling Noise Space - Change frequency of repetition of
noise lattice, can also change amplitude

Turbulence
-
produce 1/f frequency distribution
-
turbulence(pt) = noise(pt) + 1/2 noise(2*pt) + 1/4 noise(4*pt) +
....
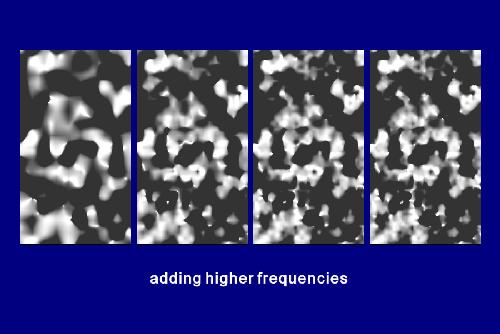
Examples
value = (sin ( point.y + turbulence(point)) +1) *.5;
color = spline (white, blue, value);
A Simple example of adding noise for marble:

Wood - use above plus turbulence added to point

Some examples of using turbulence to create the
actual object geometry/density procedurally


Nice Java Applet by
Justin Legakis
Nice
Procedural Texture Page
Ken Perlin's
Hypertexture Page
Can Apply To Other Attributes
Bump Mapping - Texture Map the Normal
to the Surface

Return to CMSC 491A/691A Notes Page



















