General Algorithm Outline
- Read in scene information and object information
- Initialize color table (using ct_gen)
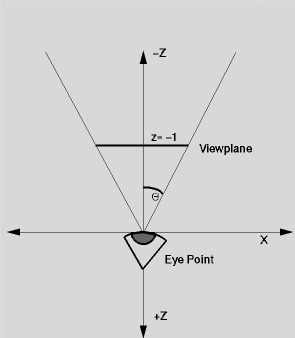
- Calculate viewing parameters and area to raytrace
- For Y = -ratio*tan(theta) to ratio*tan(theta)
- Initialize color_buffer to background color
- For X = -tan(theta) to tan(theta)
- For each object in the scene
- Test to see if ray intersects each object and
save t value of this intersection and object number if this is the closest one so far.
- Test to see if ray intersects each object and
- Shoot shadow ray for this pixel for the closest object
Shadow ray origin = Intersection point
Shadow ray direction = light - Intersection point - Shoot reflection ray for this pixel for the closest object
Reflection ray origin = Intersection point
Reflection ray direction = 2*N*(N.E) - E - Calculate the illumination and color of this object based on
the illumination model, shadow information, and reflection color.
I suggest adding Ir*ks*.5 for the reflected color. - color_buffer[x] = color from above
- For each object in the scene
- Write color_buffer to screen or file (using write_buffer cmd)
Ray Intersection
For this lab, you need to calculate the intersection of a parametric semi-infinite ray with a sphere: Let the ray be R(t) = O + D*tColor Calculation:
Use the edge library calls ct_gen and write_buffer to create
the color table and to write the scanline information for the image. See the
sample program "scan_sample.c" in the class area for examples of how to use these functions.
Use the edge library calls ct_gen and write_buffer to create the color table and to write the scanline information for the image. See the sample program "scan_sample.c" in the class area for examples of how to use these functions.
David S. Ebert
December 1998
