UMBC CMSC203, Discrete Structures, Fall 2010

Homework Assignments

Notation:

Throughout, we will use these references:

Homework 1, Due Tuesday, 09/07

  1. [Adapted from Rosen 6/e]
    State whether each of the following relationships between sets is true or false. Justify your answer briefly. (Here, ∅ is the empty set.)

    1. ∅ ∈ ∅

    2. {∅} ∈ {∅}

    3. ∅ ∈ {∅}

    4. {∅} ⊆ {∅}

    5. ∅ ⊆ ∅

  2. [Adapted from Epp 3/e]
    Let R be the set of all real numbers and let A indicate the complement of the set A. We define the sets A, B and C as follows:
    A = { x ∈ R | -3 ≤ x ≤ 0 }

    B = { x ∈ R | -1 < x < 2 }

    C = { x ∈ R | 6 < x ≤ 8 }

    Describe the following sets:

    1. A ∪ B

    2. A ∩ C

    3. A ∪ B

    4. A ∩ B

    5. A ∪ B

  3. For each of the following functions, state whether the function is one-to-one, whether the function is onto and whether the function is a bijection. Pay close attention to the domain and codomain of each function. Briefly justify your answer.

    1. f : N → N,   f (n) = n2 + 5.

    2. f : Z → Z,   f (n) = n2 + 5.

    3. f : N → N,   f (n) = 2 n + 7.

    4. f : R → R,   f (x) = 2 x + 7.

    5. f : R → R,   f (x) = 2 x3 + 1.

    Note: N, Z and R denote the set of natural numbers, integers and real numbers respectively.

  4. Read "A Mathematician's Lament" (PDF) by Paul Lockhart posted on the web site of the Mathematical Association of America. (Here's a local copy.)

    In this essay, Lockhart complains that in the standard mathematics curriculum taught in elementary school through high school "there is no actual mathematics being done in our mathematics classes" (p. 14) and that "there is surely no more reliable way to kill enthusiasm and interest in a subject than to make it a mandatory part of the school curriculum." In short, he claims that the mathematics education you have likely received so far is all wrong.

    Defend yourself! Write a convincing argument against Lockhart's position. Be persuasive. Pick apart Lockhart's argument. Support your own position with facts, personal experience, logical reasoning, etc.

    Please submit this part of your homework on its own pieces of paper as it will be graded separately from other questions.


Homework 2, Due Tuesday, 09/14

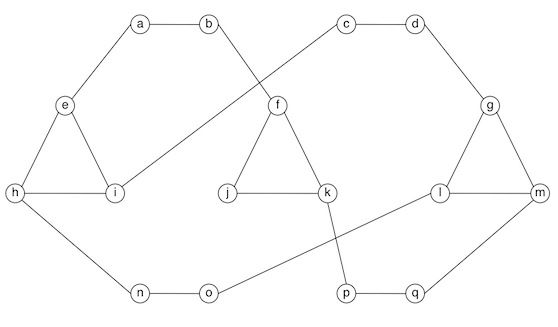
  1. Vertex Cover. Consider a graph G. Let X be a subset of the vertices in G. We say that X is a vertex cover of G if for every edge in G at least one of the endpoints of that edge is in X.

    In the graph below, find a vertex cover with as few vertices as you can. List the vertices of the vertex cover you found and briefly argue that it is the smallest possible.

    Hint: the smallest vertex cover in this graph has 10 vertices.

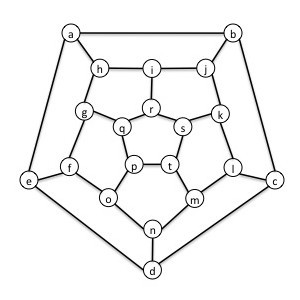
  2. Hamiltonian Circuits. [Adapted from Problem Solving Through Recreational Mathematics by Averbach & Chein, 1980.]
    A graph has a Hamiltonian circuit if there is a path in the graph that visits every vertex exactly once and returns to the first vertex in the path.
    1. Does the graph below have a Hamiltonian circuit? Justify your answer.

    2. In general, if a graph has a Hamiltonian circuit, is it necessarily the case that the graph has an Euler circuit? Justify your answer.
    3. In general, if a graph has an Euler circuit, is it necessarily the case that the graph has a Hamiltonian circuit? Justify your answer.

  3. Regular Graphs. In a d-regular graph, every vertex in the graph has degree d. Recall that the degree of a vertex is the number of edges incident on the vertex. (I.e., count the number of edges coming out of a vertex and that is its degree.)
    1. Draw a 3-regular graph with 6 vertices.
    2. Draw a 3-regular graph with 8 vertices.
    3. Draw a 3-regular graph with 10 vertices.
    4. Are there any 3-regular graphs with 9 vertices? why or why not?

Homework 3, Due Tuesday, 09/21

  1. Tautologies. Use a truth table to show that the following proposition is a tautology. You must show the intermediate steps in the truth table.
    (¬ (p ∨ q)) ⊕ ( (¬p) → q)

  2. Tautologies, again. [From Rosen 5/e.]
    Show that the following proposition is a tautology using algebraic manipulation of logical equivalences (i.e., without using a truth table). You may use the logical equivalences in Tables 5, 6 and 7 in Section 1.2 of Rosen 5/e or Tables 6, 7 and 8 in Rosen 6/e. Show all your work.
    [ ( p ∨ q) ∧ ( p → r) ∧ ( q → r) ] → r

  3. Logical Equivalences. [From Rosen 5/e.]
    Show that ¬ p → (q → r) and q → (p ∨ r) are logically equivalent without using truth tables. You may use the logical equivalences in Tables 5, 6 and 7 in Section 1.2 of Rosen 5/e or Tables 6, 7 and 8 in Rosen 6/e.

  4. Knights and Knaves. [From "A Whole Slew of Computer-Generated Knights and Knaves Puzzles" by Zac Ernst, 1999.]
    Statements made by knights are true. Statements made by knaves are false. You meet three people: Xavier, Yolanda and Zain. You know that each is either a knight or a knave. This is what they said:
    Xavier: "It is not the case that Zain is a knave."
    Yolanda: "Zain and Xavier are both knights."
    Zain: "Xavier is a knight or Yolanda is a knave."
    Which of Xavier, Yolanda and Zain are knights? which are knaves? Show your reasoning.

Homework 4, Due Tuesday, 09/28

For this homework assignment, you are asked to provide 4 proofs. Remember that proofs are written in English. You proof should not be a sequence of arithmetic equations. There must be a narrative composed of complete English sentences, correctly punctuated, with math symbols mixed in as appropriate, which convinces the reader that the claim is correct.

  1. Indirect Proof. Give an indirect proof for the following claim:
    If m and n are odd integers, then m⋅n is an odd integer.


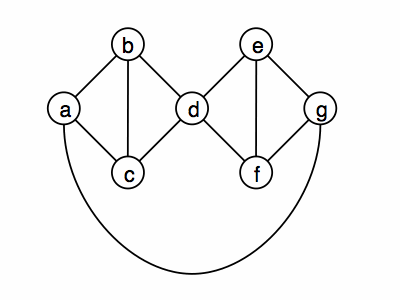
  2. Proof by Contradiction. Prove by contradiction that the following graph is not 3-colorable.


  3. Proof by Cases. [Adapted from Rosen 5/e.]
    Let min: R × R → R be the function that "returns" the minimum of two values. (Here, R is the set of real numbers.)

    For example,

    min(3.1, 5) = 3.1

    min(17.2, 9.4) = 9.4

    Prove by cases, that for all real numbers a, b and c, that

    min(min(a, b), c) = min(a, min(b, c))


  4. Equivalence Proof. [Adapted from Rosen 5/e.]
    Prove the set equality below by showing that every element of the set on the left hand side of the equality is also an element of the set on the right hand side, and vice versa. (I.e., do not prove this using algebraic identities.)
    (B − A) ∪ (C − A)  =  (B ∪ C) − A

Homework 5, Due Tuesday, 10/05

  1. Indirect Proof 2. For some function f : R → R, let g : R → R be defined by g(x) = f (x/2). (Note: here R is the set of real numbers.) Provide a well-written indirect proof which shows that if f  is one-to-one then g must also be one-to-one. Your proof must follow the indirect proof format.

  2. Arithmetic with mod. Use the repeated squaring technique to compute 9619 % 149. Show all of your work. Your work should not have any numbers bigger than 1492 = 22201.

  3. Inverses mod 29. For each integer x, 1 ≤ x < 29, find an integer y, 1 ≤ y < 29, such that
    x ⋅ y ≡ 1 (mod 29).
    In other words, x ⋅ y % 29 = 1. Then, x and y are called inverses modulo 29.

  4. A Shortcut. Fermat's Little Theorem states that if p is prime, then for any integer a not divisible by p,
    a p − 1 ≡ 1    (mod p).
    Take advantage of Fermat's Little Theorem to compute the value 95282 % 19 by noticing that 918 ≡ 1  (mod 19). Show your work.

Homework 6, Due Tuesday, 10/12

  1. GCD Proof. Let a and b be integers such that a is even and b is odd. Argue that gcd(a, b) = gcd(a/2, b).

  2. Euclid's Algorithm. Use Euclid's algorithm to compute gcd(18893511, 1154300). Show all of your work.

  3. Extended Euclid's Algorithm. Use the Extended Euclid's Algorithm to find the multiplicative inverse of 173 modulo 235012. Show all of your work. (See Notes on the Extended Euclid's Algorithm.)

  4. Chinese Remainder Theorem. Use the Chinese Remainder Theorem to find an integer x such that 0 ≤ x < 1456 and the following congruences hold:
    x ≡ 5   (mod 7)
    x ≡ 8   (mod 13)
    x ≡ 11   (mod 16)
    Note that 7 ⋅ 13 ⋅ 16 = 1456 and recall that the notation
    a ≡ b   (mod n)
    means that a % n = b % n, where % is the remainder operator. Show your work. (See notes on the Chinese Remainder Theorem.)

Homework 7, Due Tuesday, 10/19

For better typesetting, you can download this homework set in PDF: hw7.pdf.

Instructions: In the following questions you are asked to use proof by induction. Your proof must not simply be a sequence of equations, even if the statement you are proving is arithmetic in nature. Clearly indicate using complete English sentences: 1) what you are allowed to assume from the induction hypothesis, 2) what you need to show to establish the induction step, and 3) which steps of the proof uses the induction hypothesis.

Responses that do not include well-written English sentences that clearly explain your proof will receive a grade of no more than 50%.

  1. Induction (cubes). Prove by induction that for all integers n ≥ 1
    13 + 23 + 33 + ⋅⋅⋅ n3 = [ n (n+1) / 2]2

  2. Induction (fractions). Prove by induction that for all integers n ≥ 1
    1
    1⋅5
    		+
    1
    5⋅9
    		+
    1
    9⋅13
    		+  ⋅⋅⋅  +
    1
    (4 n - 3) (4 n + 1)
    		=
    n
    4 n + 1
    		.

  3. Regular Graphs, Revisited. Recall that in graph theory, a k-regular graph is an undirected graph where every vertex has degree k. Here we do not allow edges from a vertex to itself (self loops) and we do not allow more than one edge between a pair of vertices. Also recall that the degree of a vertex is simply the number of edges incident on that vertex.

    Prove by induction on k that for every k ≥ 0, there exists a k-regular graph.

  4. Induction (inequality). Let x ≥ 0 be a real number. Prove by induction on n, that for all n ≥ 2,
    1 + nx ≤ (1 + x)n.
    Hint: Do not expand (1 + x)n all the way. Use induction!

    Note: the inequality actually holds for x ≥ −1, but for this exercise you will only prove the easy case.


Homework 8, Due Tuesday, 11/02

Instructions: In the following questions you are asked to use proof by induction. Your proof must not simply be a sequence of equations, even if the statement you are proving is arithmetic in nature. Clearly indicate using complete English sentences: 1) what you are allowed to assume from the induction hypothesis, 2) what you need to show to establish the induction step, and 3) which steps of the proof uses the induction hypothesis.

Responses that do not include well-written English sentences that clearly explain your proof will receive a grade of no more than 50%.

  1. Fibonacci Numbers. [Adapted from Rosen 5/e]
    The Fibonacci numbers f0,  f1,  f2, ... are defined recursively by f0 = 0,  f1 = 1,  f2 = 1 and for all n ≥ 3,
    fn = fn − 1 + fn − 2 .
    Use structural induction to show that
    ( f1 )2 + ( f2 )2 + ⋅⋅⋅ + ( fn )2 = fn fn+1

  2. String Reversal. [Adapted from Rosen 5/e]
    In this problem, we consider only strings over {0, 1} of length greater than or equal to 0. For example, the string 01001 is a string of length 5. We use λ to denote the empty string. For a string w, we can define the reversal of the string, written wR, as follows: For example, we can unwind the recursive definition of 01001R by:
    01001R = 1001R0 = 001R10 = 01R010 = 1R0010 = λR10010 = λ10010 = 10010.
    Use structural induction to prove that for all strings w and x, (w x)R = xR wR.

    Note: For this problem, you may assume without proof that string concatenation is associative. So, given 3 strings x, y and z,  ( x y ) z = x ( y z ).

  3. Tournament Graphs. [Adapted from Rosen 5/e]
    Recall that a tournament graph G is a directed graph (without self loops) such that for any two distinct vertices u and v in G, exactly one of (u, v) or (v, u) is an edge in G. (Here, u and v being distinct means u ≠ v.)

    You can think of the vertices of a tournament graph as teams participating in a round-robin tournament (where each team plays every other team once) in a sport that does not allow tie games. Then, for any two teams u and v, either u defeats v or v defeats u (but not both). If u defeats v, then the edge (u, v) is placed in the graph. Otherwise, v defeats u and (v, u) is placed in the graph.

    In this problem, you are asked to prove by induction that every tournament graph G has a "winner". Here, a winner is a vertex w that defeats every vertex (other than w) either directly or indirectly. We say that w defeats x directly if (w, x) is an edge in G. Vertex w defeats vertex x indirectly if there exists a vertex u such that (w, u) and (u, x) are edges in G (that is, w defeats u which in turn defeats x).

    Note: a tournament graph can have more than one winner.

    Hint: for a vertex v think about the set of vertices that v defeats directly and a second set of vertices that v defeats indirectly but not directly.


Homework 9, Due Tuesday, 11/09

For each of these questions, you must show your work and explain your answer. Answers that consist of a single number will receive fewer than 50% credit.

When factorials are involved, leave your answer in terms of factorials (e.g., 5!/(3! ⋅ 2)).

  1. Trip Planning. For a trip, you packed 2 pairs of sneakers, 3 pairs of jeans, 4 pairs of shorts, 5 shirts, 2 sweaters and 3 rings. How many different outfits can you make from the clothing you packed, if an "outfit" consists of 1 pair of sneakers, 1 pair of jeans or shorts (but not both), 1 shirt, at most 1 sweater and any number of rings? (Note: wearing rings on different fingers does not count as a different "outfit.")

    Note: Assume that your sneakers, jeans, shorts, shirts, sweaters and rings are distinguishable.

  2. Sock Drawer. Suppose your sock drawer has 17 pairs of socks that are black, white or tan. Which of the following statements must be true? Justify your answer.

    1. There are at least 5 pairs of black socks, at least 5 pairs of white socks and at least 5 pairs of tan socks.

    2. There are at most 4 pairs of black socks, at most 4 pairs of white socks or at most 4 pairs of tan socks.

    3. There are at least 6 pairs of black socks, at least 6 pairs of white socks or at least 6 pairs of tan socks.

  3. Another Sock Drawer. Suppose that your sock drawer has 6 pairs of black socks, 5 pairs of white socks and 6 pairs of tan socks. How many different ways are there to pack 5 pairs of socks? You can bring as many pairs of socks of each color as you want. Assume that socks of the same color are not distinguishable.

  4. Hotel Room Closet. In the hotel room, you hang up in the closet the 5 shirts and 2 sweaters that you packed. How many ways can you arrange the shirts and sweaters in the closet (from left to right) so that the 2 sweaters are adjacent to each other? (As before, assume that your shirts and sweaters are distinguishable.)


Homework 10, Due Tuesday, 11/16

For each of these questions, you must show your work and explain your answer. Answers that consist of a single number will receive fewer than 50% credit.

When factorials are involved, leave your answer in terms of factorials (e.g., 5!/(3! ⋅ 2)).

  1. Dog Sled Team. We wish to form a sled dog team with 7 dogs chosen from a group of 14 Siberian Huskies and 9 Alaskan Malamutes. How many different teams can be formed if we must have more Siberian Huskies than Alaskan Malamutes?
    Note: in this question the dogs are considered individuals and are distinguishable.

  2. Car Park. There are 4 red cars and 7 blue cars parked in 11 consecutive spots of a parking lot. Each car is distinguishable by its license plate.
    1. How many ways can the cars be parked in these 11 spots so the 4 red cars are adjacent to each other?
    2. How many ways can the cars be parked in these 11 spots so none of the 4 red cars is adjacent to another red car?

  3. Marble Placement. In a board game, you have 19 indistinguishable marbles that you can place in 5 distinguishable locations. You must place at least 2 marbles at each location, but are otherwise allowed to place as many or as few marbles at each location. How many different ways can you make these placements?

  4. Balls & Bins. You have 13 balls that you throw at 5 bins labeled A, B, C, D and E. Our assumption is that when a ball is thrown at the bins, there is an equal probability that the ball lands in any particular bin. Also, the ball will always land in one of the bins. Each bin is large enough to hold any number of balls.
    1. You throw the 13 balls, one at a time, at the bins. What is the probability that exactly 3 balls land in bin A? Justify your answer.
    2. You throw the 13 balls, one at a time, at the bins. What is the probability that 4 or fewer balls land in bin B? Justify your answer.

Homework 11, Due Tuesday, 11/23

For each of these questions, you must show your work and explain your answer. Answers that consist of a single number will receive fewer than 50% credit.

  1. Two Urns. [Adapted from Epp, 3/e.]
    You have two urns. One urn holds 5 red balls and 13 yellow balls. The second urn holds 9 red balls and 11 yellow balls. You pick one ball using this procedure: randomly pick one of the two urns with equal probability, then pick a ball from the chosen urn so that each ball is chosen with equal probability.
    1. What is the probability that the chosen ball is red?
    2. If the chosen ball is red, what is the probability that the chosen ball came from the first urn?

  2. Independent Dice. A standard 6-sided die has faces numbered 1, 2, 3, 4, 5 and 6. Assume that it is equally likely for each of the faces to be on top when the die is rolled. Suppose that you roll 2 six sided dice and add the two numbers that appear on top. Let E be the event that the sum of the two dice is divisible by 3. Let F be the event that the sum is less than or equal to 6. Are events E and F independent?

  3. Odd Man Out. Four friends play a game called Odd Man Out. They each flip a fair coin. If 1 person has heads and the other 3 have tails, then the person with heads is the odd man. Similarly, if 1 person has tails and the other 3 have heads, then the person with tails is the odd man. What is the probability of having an odd man after each person flips just once? Explain your answer.

  4. Odd Man Out, Part Deux. Suppose the four friends in the question above continue playing Odd Man Out until someone becomes the odd man. What is the expected number of times that they have to play this game? Explain your answer.

Homework 12, Due Thursday, 12/02

Note: this assignment is due on Thursday after Thanksgiving (not Tuesday).

  1. 4- and 8-sided Dice. You have a fair 4-sided die and a fair 8-sided die. (Here a die is fair if when the die is rolled, there is an equal probability for any particular side to be on top.) The sides of the 4-sided die are labeled with 2, 7, 9 and 12. The sides of the 8-sided die are labeled with 1, 2, 3, 4, 7, 8, 9 and 10.
    Note: Show all of your work and explain your answers.

    1. What is the expected value of the number on top when you roll the 4-sided die?

    2. What is the expected value of the number on top when you roll the 8-sided die?

    3. What is the expected value of the sum of the numbers on top when you roll both dice?

  2. Plastic Utensils. You randomly pick utensils from a box with plastic knives, forks and spoons. Each time you pick, there is an equal probability of picking any of the utensils remaining in the box. Initially, the box holds 4 forks, 3 spoons and 7 knives.
    Note: Show all of your work and explain your answers.

    1. Suppose you pick 3 utensils without replacement. What is the probability that you picked a fork, a spoon and a knife (in any order)?

    2. Suppose that you pick 2 utensils without replacement. What is the conditional probability that the second utensil you picked is a knife?

    3. Suppose that you pick 2 utensils without replacement. What is the conditional probability that the second utensil you picked is a knife given that the first utensil is a fork?

    4. Suppose that you pick 2 utensils without replacement. What is the probability that at least one of the two is a spoon?

Homework 13, Due Thursday, 12/09

  1. Relations and Properties. For each of the following relations, state whether relation is reflexive, symmetric, antisymmetric and transitive. Briefly justify your response in each case.

    Note: a relation R on A is antisymmetric if for all (a, b) ∈ A × A, (a, b) ∈ R and (b, a) ∈ R implies that a = b.

    1. R1 = { (a, b) | a and b are integers and a = 3b }

    2. R2 = { (a, b) | a and b are integers and | a − b | is even }

    3. R3 = { (a, b) | a and b are integers and a b = 0 }

  2. Combining Equivalence Relations. [From Rosen 5/e.]
    Suppose that R1 and R2 are both equivalence relations on A.

    1. Must R1 ∩ R2 be an equivalence relation? Give a proof or a counterexample.

    2. Must R1 ⊕ R2 be an equivalence relation? Give a proof or a counterexample.
      Note: For two sets A and B, A ⊕ B is the symmetric difference of A and B. That is, A ⊕ B = (A − B) ∪ (B − A) .

  3. Partial Orders. Consider the set A = { 2, 5, 6, 8, 10, 24, 30, 120 } and the relation R on A defined by:
    R = { (a, b) | a divides b }.
    Since R is reflexive, antisymmetric and transitive, it is a partial order.

    1. Draw a Hasse diagram for R.

    2. List two incomparable elements in R

    3. What are the minimal and maximal elements of this partial order?

    4. Does R have a greatest element? Why or why not?

    5. Does R have a least element? Why or why

Last Modified: 22 Jul 2024 11:29:46 EDT by Richard Chang
to Fall 2010 CMSC 203 Homepage