CMSC 202 Lecture Notes: Trees

These notes discuss trees in general, not just binary trees.

Basics

Some basic terminology for trees:

Trees are formed from nodes and edges. Nodes are sometimes called vertices. Edges are sometimes called branches.
Nodes may have a number of properties including value and label.
Edges are used to relate nodes to each other. In a tree, this relation is called "parenthood."
An edge {a,b} between nodes a and b establishes a as the parent of b. Also, b is called a child of a.
Although edges are usually drawn as simple lines, they are really directed from parent to child. In tree drawings, this is top-to-bottom.
Informal Definition: a tree is a collection of nodes, one of which is distinguished as "root," along with a relation ("parenthood") that is shown by edges.
Formal Definition: This definition is "recursive" in that it defines tree in terms of itself. The definition is also "constructive" in that it describes how to construct a tree.
1. A single node is a tree. It is "root."
2. Suppose N is a node and T₁, T₂, ..., T_k are trees with roots n₁, n₂, ...,n_k, respectively. We can construct a new tree T by making N the parent of the nodes n₁, n₂, ..., n_k. Then, N is the root of T and T₁, T₂, ..., T_k are subtrees.

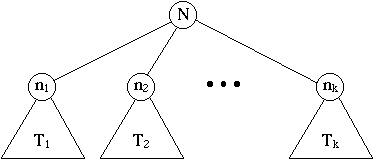
The tree T, constructed using k subtrees

More terminology

Definition: A path is a sequence of nodes n₁, n₂, ..., n_k such that node n_i is the parent of node n_i+1 for all 1 <= i <= k.
Definition: The length of a path is the number of edges on the path (one less than the number of nodes).
Definition: The descendents of a node are all the nodes that are on some path from the node to any leaf.
Definition: The ancestors of a node are all the nodes that are on the path from the node to the root.
Definition: The depth of a node is the length of the path from root to the node. The depth of a node is sometimes called its level.
Definition: The height of a node is the length of the longest path from the node to a leaf.
Definition: the height of a tree is the height of its root.

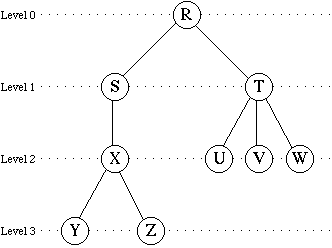
A general tree, showing node depths (levels)

In the example above:

The nodes Y, Z, U, V, and W are leaf nodes.
The nodes R, S, T, and X are internal nodes.
The degree of node T is 3. The degree of node S is 1.
The depth of node X is 2. The depth of node Z is 3.
The height of node Z is zero. The height of node S is 2. The height of node R is 3.
The height of the tree is the same as the height of its root R. Therefore the height of the tree is 3.
The sequence of nodes R,S,X is a path.
The sequence of nodes R,X,Y is not a path because the sequence does not satisfy the "parenthood" property (R is not the parent of X).

Definition: A binary tree is a tree in which each node has degree of exactly 2 and the children of each node are distinguished as "left" and "right." Some of the children of a node may be empty.
Formal Definition: A binary tree is:
1. either empty, or
2. it is a node that has a left and a right subtree, each of which is a binary tree.
Definition: A full binary tree (FBT) is a binary tree in which each node has exactly 2 non-empty children or exactly two empty children, and all the leaves are on the same level. (Note that this definition differs from the text definition).
Definition: A complete binary tree (CBT) is a FBT except, perhaps, that the deepest level may not be completely filled. If not completely filled, it is filled from left-to-right.
A FBT is a CBT, but not vice-versa.

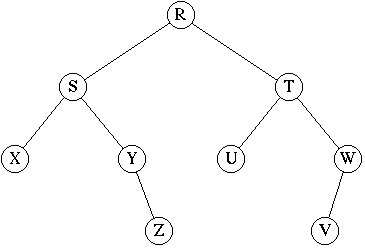
A Binary Tree. As usual, the empty children are not explicitly shown.

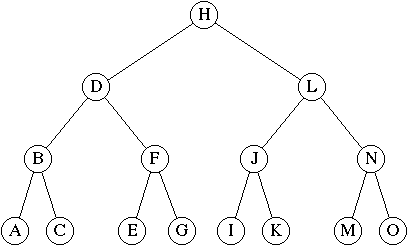
A Full Binary Tree. In a FBT, the number of nodes at level i is 2ⁱ.

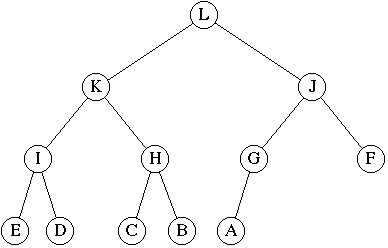
A Complete Binary Tree.

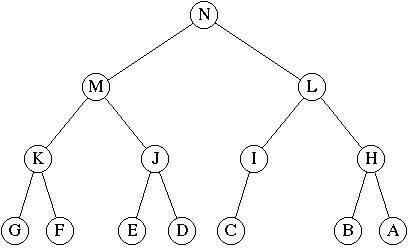
Not a Complete Binary Tree. The tree above is not a CBT because the deepest level is not filled from left-to-right.

Thomas A. Anastasio, Tue Oct 28 11:01:25 EST 1997

Modified some by Richard Chang, Tue Apr 28 12:43:27 EDT 1998.