CMSC--202 , Section Computer Science II for Majors
Fall 1997 11 October 1997 Handout -- Trees
This handout discusses trees in general, not just binary trees.
- A node is either internal or it is a leaf.
- A leaf is a node that has no children.
- Every node in a tree (except root) has exactly one parent.
- The degree of a node is the number of children it can
have.
- The degree of a tree is the maximum degree of all of its
nodes.
- Definition: A path is a sequence of nodes
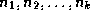 such that node
such that node 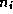 is the parent of node
is the parent of node
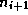 for all
for all 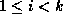 .
.
- Definition: The length of a path is the number of edges on
the path (one less than the number of nodes).
- Definition: The descendents of a node are all the nodes
that are on some path from the node to any leaf.
- Definition: The ancestors of a node are all the nodes
that are on the path from the node to the root.
- Definition: The depth of a node is the length of the path
from root to the node. The depth of a node is sometimes called its
level.
- Definition: The height of a node is the length of the
longest path from the node to a leaf.
- Definition: the height of a tree is the height of its
root.
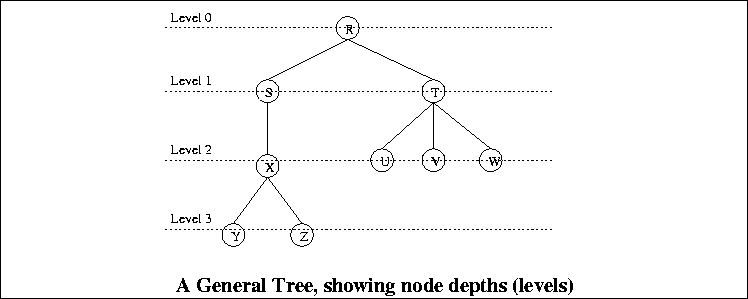
- The nodes
Y, Z, U, V, and W
are leaf nodes.
- The nodes
R, S, T, and X are
internal nodes.
- The degree of node
T is 3. The degree of node S
is 1.
- The depth of node
X is 2. The depth of node Z is
3.
- The height of node
Z is zero. The height of node
S is 2. The height of node R is 3.
- The height of the tree is the same as the height of its root
R. Therefore the height of the tree is 3.
- The sequence of nodes
R,S,X is a path.
- The sequence of nodes
R,X,Y is not a path because the
sequence does not satisfy the ``parenthood'' property (R is not
the parent of X).
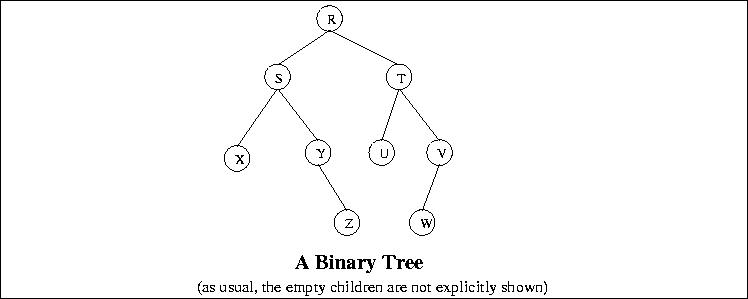
- Definition: A binary tree is a tree in which each node has
degree of exactly 2 and the children of each node are distinguished as
``left'' and ``right.'' Some of the children of a node may be empty.
- Formal Definition: A binary tree is:
- either empty, or
- it is a node that has a left and a right subtree, each of which
is a binary tree.
- Definition: A full binary tree (FBT) is a binary
tree in which each node has exactly 2 non-empty children or exactly
two empty children, and all the leaves are on the same level. (Note
that this definition differs from the text definition).
- Definition: A complete binary tree (CBT) is a FBT
except, perhaps, that the deepest level may not be completely filled.
If not completely filled, it is filled from left-to-right.
- A FBT is a CBT, but not vice-versa.
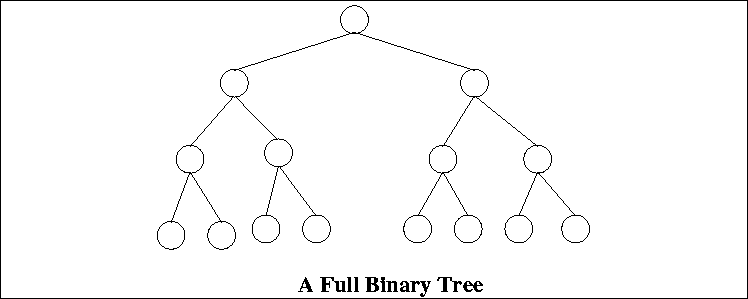
- Note that in a FBT, the number of nodes at level i is
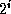 .
.
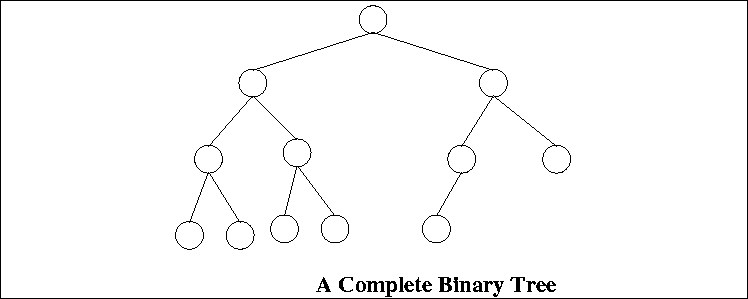

- The above tree is not a CBT because the deepest level is
not filled from left-to-right.
Thomas A. Anastasio
Tue Oct 28 11:01:25 EST 1997
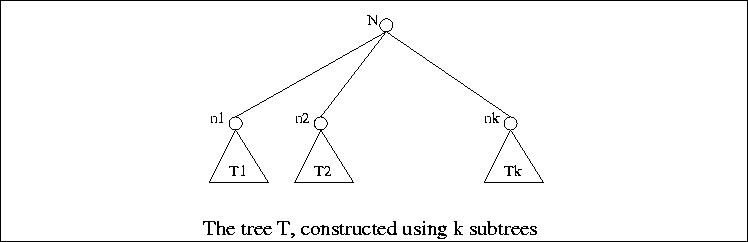
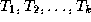 are trees with
roots
are trees with
roots 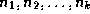 , respectively. We can construct a new
tree T by making N be the parent of the nodes
, respectively. We can construct a new
tree T by making N be the parent of the nodes
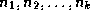 . Then, N is the root of T and
. Then, N is the root of T and
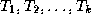 are subtrees.
are subtrees.

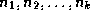 such that node
such that node 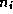 is the parent of node
is the parent of node
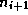 for all
for all 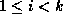 .
.



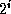 .
.

