- comparison-based sorting, and
- address-calculation-based sorting
-
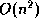 algorithms
algorithms
- bubblesort
- insertion sort
- selection sort
-
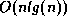 algorithms
algorithms
- merge sort
- quick sort (average behavior)
- heap sort
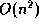 algorithm.
algorithm.
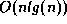
CMSC--202 Computer Science II for Majors
Fall 1997 5 November 1997 Introduction to Sorting
This handout documents some of the material covered in the sorting lectures.
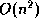 algorithms
algorithms
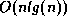 algorithms
algorithms
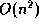 algorithm.
algorithm.
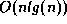
Definition: A comparison tree (also known as a
decision tree) is a binary tree in which, at each internal node,
a comparison is made between two keys and in which each leaf
represents a sorted arrangement of keys.
The number of leaves in a comparison tree must be  , where n is
the number of items to be sorted. This is the number of permutations
of the n items. Every permutation must be represented in the
comparison tree, and every leaf represents one of the permutations.
, where n is
the number of items to be sorted. This is the number of permutations
of the n items. Every permutation must be represented in the
comparison tree, and every leaf represents one of the permutations.
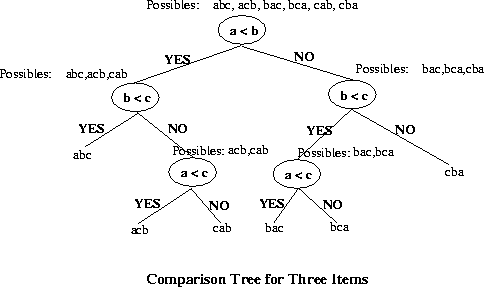
The ``worst-case'' number of comparisons in the tree is the length of
the longest path. For the three item tree above, the longest path is
of length 3. This can be expressed as the ceiling of 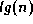 The ``average'' number of comparisons is just the sum of the path
lengths divided by the number of leaves or
The ``average'' number of comparisons is just the sum of the path
lengths divided by the number of leaves or
(2 + 3 + 3 + 3 + 3 + 2) / 6 = 2.67
It can be shown that as n increases, the average number of
comparisons grows proportionately to 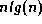 . Thus, the very best
average performance of any sorting algorithm based on comparisons is
. Thus, the very best
average performance of any sorting algorithm based on comparisons is
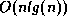 Question: Since mergesort is an
Question: Since mergesort is an 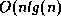 algorithm and selection
sort is an
algorithm and selection
sort is an 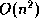 algorithm, why would one ever choose the
``slower'' selection sort over the ``faster'' mergesort?
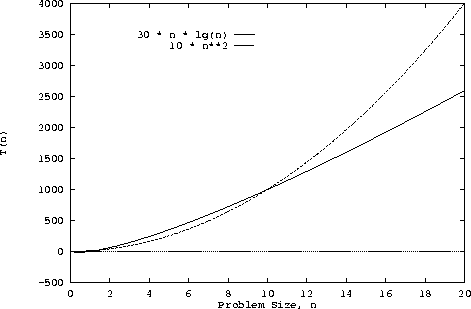
Answer: selection sort will probably be faster than mergesort
when n is not large. It's a simpler algorithm so will likely have a
lower constant of proportionality than mergesort. The following
figure shows an example.
algorithm, why would one ever choose the
``slower'' selection sort over the ``faster'' mergesort?
Answer: selection sort will probably be faster than mergesort
when n is not large. It's a simpler algorithm so will likely have a
lower constant of proportionality than mergesort. The following
figure shows an example.
Question: Since mergesort and quicksort are each 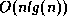 algorithms, why choose one over the other?
Answer: quicksort runs faster on average, even though both have
the same growth behavior with increasing n.
Question: Well, then, why ever use mergesort?
Answer: The average performance of quicksort is
algorithms, why choose one over the other?
Answer: quicksort runs faster on average, even though both have
the same growth behavior with increasing n.
Question: Well, then, why ever use mergesort?
Answer: The average performance of quicksort is 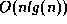 ,
but there are worst cases which produce
,
but there are worst cases which produce 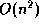 performance.
Mergesort performance is the same for average and worst cases. If you
don't want to take the chance that your data may give the worst case
for quicksort, you might want to choose mergesort (or some other
performance.
Mergesort performance is the same for average and worst cases. If you
don't want to take the chance that your data may give the worst case
for quicksort, you might want to choose mergesort (or some other
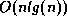 algorithm).
algorithm).