bintrees.h interface file for the binary tree operations
is in the directory
anastasi/Public/202/Includes .
The implementation of the operations
is in the lib202.a archive in the directory
anastasi/Public/202/Libraries .
CMSC--202 , Section Computer Science II for Majors
Fall 1997 16 November 1997 Handout -- Binary Trees
We have already examined the mathematical notion of trees in
general and binary trees in particular. We now interpret those
mathematical ideas to a form useful for computation by developing
a binary tree ADT.
A binary tree is a homogeneous collection of hierarchically
organized data. Each datum contains a value, a left
child, and a right child (both of which are data). The value
stored at a datum is of type tree_item_type and a tree is of
type tree_type. There is a constant the_empty_tree that
designates a binary tree containing no data. The following non-destructive
operations are defined:
tree_type tree_cons(tree_item_type E, tree_type L, tree_type R)
constructs and returns a new tree with E as its root
and L and R as its left and right children, respectively.
tree_item_type tree_data(tree_type T) returns the value
at the root of T. It is an error to invoke tree_data on an empty
tree.
tree_type left_child(tree_type T) returns the left subtree of
T. It is an error to invoke left_child on an empty tree.
tree_type right_child(tree_type T) returns the right subtree of
T. It is an error to invoke right_child on an empty tree.
BOOL empty_tree(tree_type T) returns TRUE if T is empty,
FALSE otherwise.
The bintrees.h interface file for the binary tree operations
is in the directory
anastasi/Public/202/Includes .
The implementation of the operations
is in the lib202.a archive in the directory
anastasi/Public/202/Libraries .
This section presents one implementation of the binary tree ADT
presented above. This implementation follows closely our
implementation of linked lists. We assume that tree_item_type
has been defined to be the type of object we want to store at each
node of the tree. The underlying data structures are defined as follows:
typedef struct tree_tag *tree_type;
typedef struct tree_tag {
tree_item_type data;
tree_type left;
tree_type right;
} tree_struct_type;
Because a tree is a pointer in this implementation, it is natural to
use NULL to represent the empty tree:
#define the_empty_tree NULL
The code for the five basic functions is straightforward; comparison with the list routines presented in class reveals an almost token--for--token similarity:
tree_type
tree_cons(tree_item_type value, tree_type left, tree_type right)
{
tree_type result;
result = (tree_type) malloc(sizeof(tree_struct_type));
assert(result != NULL);
result->data = value;
result->left = left;
result->right = right;
return result;
}
tree_item_type
tree_data(tree_type tree)
{
assert(empty_tree(tree) == FALSE);
return tree->data;
}
tree_type
left_child(tree_type tree)
{
assert(empty_tree(tree) == FALSE);
return tree->left;
}
tree_type
right_child(tree_type tree)
{
assert(empty_tree(tree) == FALSE);
return tree->right;
}
BOOL
empty_tree(tree_type tree)
{
return (tree == the_empty_tree) ? TRUE : FALSE;
}
A traversal routine is one that visits every node of a tree, performing a given operation on each node when it is visited. Three orderings of the nodes during traversal are in common use:
The following code will perform any one of these traversal methods:
typedef enum {preorder, inorder, postorder} traversal_type;
void
traversal(tree_type tree, traversal_type method, void (*operation)(tree_type))
{
if (empty_tree(tree) == FALSE)
{
if (method == preorder)
operation(tree);
traversal(left_child(tree), method, operation);
if (method == inorder)
operation(tree);
traversal(right_child(tree), method, operation);
if (method == postorder)
operation(tree);
}
}
As an example of the use of the traversal routine, the
following code will print the contents of a tree of integers:
void
print_int_tree_data(tree_type tree)
{
printf("%d ", tree_data(tree));
}
void
print_int_tree(tree_type tree, traversal_type type)
{
traversal(tree, type, print_int_tree_data);
putchar('\n');
}
A search is like a traversal, except that when a desired node in the
tree is encountered, the search is terminated. A search returns the
desired node, or the_empty_tree if no appropriate node is
found.
Two orderings of the nodes in a search are in common use:
Each of the search routines in the following subsections takes two arguments: a tree to search, and a predicate that determines whether an acceptable node has been found.
Here is an implementation of depth--first search. It uses recursion to search downward in the tree:
tree_type
depth_first_search(tree_type tree, BOOL (*predicate)(tree_type))
{
tree_type result;
if (empty_tree(tree) == TRUE)
return the_empty_tree;
if (predicate(tree) == TRUE)
return tree;
result = depth_first_search(left_child(tree), predicate);
if (empty_tree(result) == FALSE)
return result;
else
return depth_first_search(right_child(tree), predicate);
}
Here is an implementation of depth--first search that uses an explicit stack. The stack is used to keep track of which nodes are yet to be examined:
tree_type
dfs_stack(tree_type tree, BOOL (*predicate)(tree_type))
{
stack_type stack = create_stack();
tree_type guess;
push(tree, stack);
while (empty_stack(stack) == FALSE)
{
guess = pop(stack);
if (empty_tree(guess) == TRUE)
continue;
if (predicate(guess) == TRUE)
return guess;
push(left_child(guess), stack);
push(right_child(guess), stack);
}
return the_empty_tree;
}
Here is an implementation of breadth--first search. Notice that a queue is used instead of a stack; otherwise, this routine is virtually identical to the second implementation of depth--first search:
tree_type
bfs_queue(tree_type tree, BOOL (*predicate)(tree_type))
{
queue_type queue = create_queue();
tree_type guess;
enqueue(tree, queue);
while (empty_(queue) == FALSE)
{
guess = dequeue(queue);
if (empty_tree(guess) == TRUE)
continue;
if (predicate(guess) == TRUE)
return guess;
enqueue(left_child(guess), queue);
enqueue(right_child(guess), queue);
}
return the_empty_tree;
}
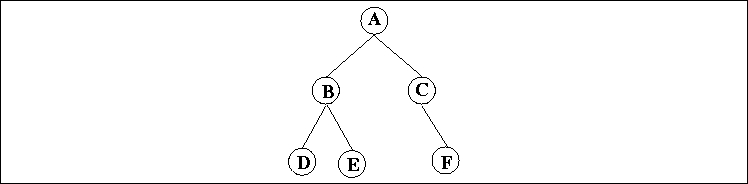 it might return the tree:
it might return the tree:
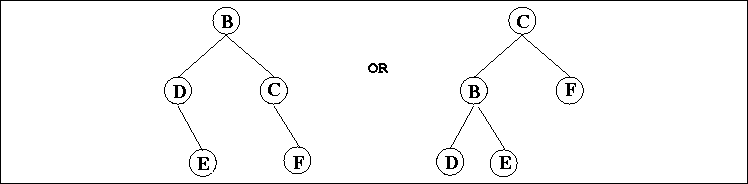 Note that other solutions are possible; your program may return any legal
solution. If delete_root is called on the empty tree, or
on a tree containing exactly one node, it should return the empty tree.
Delete_root must not modify its argument in any way; it
should produce a brand new tree.
Note that other solutions are possible; your program may return any legal
solution. If delete_root is called on the empty tree, or
on a tree containing exactly one node, it should return the empty tree.
Delete_root must not modify its argument in any way; it
should produce a brand new tree.