CMSC--202 Computer Science II for Majors
Fall 1997 13 November 1997 Asymptotic Analysis
A programmer usually has a choice of data structures and algorithms to
use. Choosing the best one for a particular job involves, among other
factors, two important measures:
- Time Complexity: how much time will the program take?
- Space Complexity: how much storage will the program need?
A programmer will sometimes seek a tradeoff between space and time
complexity. For example, a programmer might choose a data structure
that requires a lot of storage in order to reduce the computation time.
There is an element of art in making such tradeoffs, but
the programmer must make the choice from an informed point of view.
The programmer must have some verifiable basis on which to make the
selection of a data structure or algorithm. Complexity analysis
provides such a basis.
Complexity refers to the rate at which the storage or time grows as a
function of the problem size. The absolute growth depends on the machine
used to execute the program, the compiler used to construct the
program, and many other factors. We would like to have a way of
describing the inherent complexity of a program (or piece of a
program), independent of machine/compiler considerations. This means
that we must not try to describe the absolute time or storage needed.
We must instead concentrate on a ``proportionality'' approach,
expressing the complexity in terms of its relationship to some known
function. This type of analysis is known as asymptotic analysis.
Asymptotic analysis is based on the idea that as the problem size
grows, the complexity can be described as a simple proportionality to
some known function. This idea is incorporated in the ``Big Oh''
notation for asymptotic performance.
Definition:  if and only if there are constants
if and only if there are constants
 and
and  such that
such that  for all
for all  .
The expression
.
The expression  is read as ``T of n is in BigOh of f of n.''
BigOh is sometimes said to describe an ``upper-bound'' on the
complexity. Other forms of asymptotic analysis (``BigOmega'',
``LittleOh'', ``BigTheta'') are similar in spirit to BigOh, but will
not be discussed in this handout.
is read as ``T of n is in BigOh of f of n.''
BigOh is sometimes said to describe an ``upper-bound'' on the
complexity. Other forms of asymptotic analysis (``BigOmega'',
``LittleOh'', ``BigTheta'') are similar in spirit to BigOh, but will
not be discussed in this handout.
If a function  , then eventually the value
, then eventually the value  will
exceed the value of
will
exceed the value of  . ``Eventually'' means ``after n
exceeds some value.'' Does this really mean anything useful? We might
say (correctly) that
. ``Eventually'' means ``after n
exceeds some value.'' Does this really mean anything useful? We might
say (correctly) that  , but we don't get a lot of
information from that;
, but we don't get a lot of
information from that;  is simply too big. When we use BigOh
analysis, we implicitly agree that the function
is simply too big. When we use BigOh
analysis, we implicitly agree that the function  we choose is
the smallest one that still satisfies the definition. It is correct
and meaningful to say
we choose is
the smallest one that still satisfies the definition. It is correct
and meaningful to say  ; this tells us
something about the growth pattern of the function
; this tells us
something about the growth pattern of the function  , namely
that the
, namely
that the  term will dominate the growth as n increases.
The following functions are often encountered in computer science BigOh
analysis:
term will dominate the growth as n increases.
The following functions are often encountered in computer science BigOh
analysis:
-
 . This is called constant growth.
. This is called constant growth.  does not grow at all as a function of n, it is a constant. It is
pronounced ``BigOh of one.'' For example, array access has this
characteristic.
does not grow at all as a function of n, it is a constant. It is
pronounced ``BigOh of one.'' For example, array access has this
characteristic. A[i] takes the same time no matter how big
A is.
-
 . This is called logarithmic growth.
. This is called logarithmic growth.  grows as the base 2 logarithm of n (actually, the base doesn't
matter, it's just traditional to use base-2 in computer science).
It is pronounced ``BigOh of log n.'' For example, binary search has
this characteristic.
grows as the base 2 logarithm of n (actually, the base doesn't
matter, it's just traditional to use base-2 in computer science).
It is pronounced ``BigOh of log n.'' For example, binary search has
this characteristic.
-
 . This is called linear growth.
. This is called linear growth.  grows
linearly with n. It is pronounced ``BigOh of n.'' For example,
looping over all the elements in a one-dimensional array would be an
grows
linearly with n. It is pronounced ``BigOh of n.'' For example,
looping over all the elements in a one-dimensional array would be an
 operation.
operation.
-
 . This is called ``n log n'' growth.
. This is called ``n log n'' growth.  grows as n times the base 2 logarithm of n. It is pronounced
``BigOh of n log n.'' For example, heapsort and mergesort have this
characteristic. In fact, no sorting algorithm that uses comparison
between elements can be faster than
grows as n times the base 2 logarithm of n. It is pronounced
``BigOh of n log n.'' For example, heapsort and mergesort have this
characteristic. In fact, no sorting algorithm that uses comparison
between elements can be faster than  .
.
-
 . This is called polynomial growth.
. This is called polynomial growth.  grows
as the k-th power of n. In computer science, k is rarely
greater than 3. For example, selection sort is an
grows
as the k-th power of n. In computer science, k is rarely
greater than 3. For example, selection sort is an  algorithm.
It is pronounced ``BigOh of n squared.''
algorithm.
It is pronounced ``BigOh of n squared.''
-
 . This is called exponential growth.
. This is called exponential growth.  grows exponentially. It is pronounced ``BigOh of 2 to the n.''
Exponential growth is the most-feared growth pattern in computer
science; algorithms that grow this way are basically useless for
anything but very small problems.
grows exponentially. It is pronounced ``BigOh of 2 to the n.''
Exponential growth is the most-feared growth pattern in computer
science; algorithms that grow this way are basically useless for
anything but very small problems.
The growth patterns above have been listed in order of increasing
``size.'' That is,
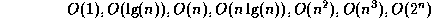
Note that it is not true that if  then
then  . The ``='' sign does not mean equality in the usual
algebraic sense -- that's why it is pronounced ``
. The ``='' sign does not mean equality in the usual
algebraic sense -- that's why it is pronounced `` is in BigOh
of
is in BigOh
of  ,'' and not ``
,'' and not `` equals BigOh of
equals BigOh of  ,''
,''
Suppose we have a program that takes some constant amount of time
to set up, then grows linearly with the problem size n. The
constant time might be used to prompt the user for a filename and open
the file. Neither of these operations are dependent on the amount of
data in the file. After these setup operations, we read the data from
the file and do something with it (say print it). The amount of time
required to read the file is certainly proportional to the amount of
data in the file. We let n be the amount of data. This program has
time complexity of  . To see this, let's assume that the setup
time is really long, say 500 time units. Let's also assume that the
time taken to read the data is 10 n, 10 time units for each data
point read. The following graph shows the function 500 + 10 n
plotted against n, the problem size. Also shown are the functions
n and 20 n.
. To see this, let's assume that the setup
time is really long, say 500 time units. Let's also assume that the
time taken to read the data is 10 n, 10 time units for each data
point read. The following graph shows the function 500 + 10 n
plotted against n, the problem size. Also shown are the functions
n and 20 n.

Note that the function n will never be larger than the
function 500 + 10 n, no matter how large n gets. However, there
are constants  and
and  such that
such that  when
when
 . One choice for these constants is
. One choice for these constants is  and
and  .
Therefore,
.
Therefore,  . (There are, of course, other choices
for
. (There are, of course, other choices
for  ; any value of
; any value of  will do.)
will do.)
Here we look at the functions  , n,
, n,  ,
,  ,
,  ,
and
,
and  to get some idea of their relative ``size.''
In the first graph, it looks like
to get some idea of their relative ``size.''
In the first graph, it looks like  and
and  are larger than
are larger than  . They're not; the second graph shows
the same data on an expanded scale. Clearly
. They're not; the second graph shows
the same data on an expanded scale. Clearly  when n > 4 and
when n > 4 and  when n > 10.
when n > 10.


The following table shows how long it would take to perform  steps on a computer that does 1 billion steps/second.
steps on a computer that does 1 billion steps/second.
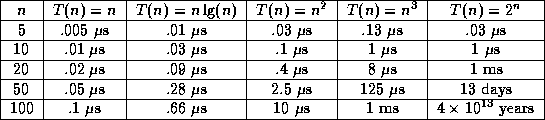
Notice that when  , the compute time for
, the compute time for  has
started to become too large to be practical. This is most certainly
true when
has
started to become too large to be practical. This is most certainly
true when  . Even if we were to increase the speed of the
machine a million-fold,
. Even if we were to increase the speed of the
machine a million-fold,  for n = 100 would be 40,000,000 years,
a bit longer than you might want to wait for an answer.
for n = 100 would be 40,000,000 years,
a bit longer than you might want to wait for an answer.
As a final example, we look at the list implementation of
queue. In this implementation, each enqueue operation
requires traversing the entire list to find the end, then
``attaching'' the new item at the end. What is the asymptotic time
complexity of this operation as a function of n, the number of items
in the queue?
First of all, to find the end of the list, we must traverse the entire
list. This takes n operations (one rest operation for each
item on the list). Therefore, a single enqueue operation has
asymptotic complexity  .
But, suppose we enqueue n items, one after another? The asymptotic
complexity will be
.
But, suppose we enqueue n items, one after another? The asymptotic
complexity will be  . You may object that the list is
not n long until all n items have been enqueued. Look at it this
way; the first item takes one operation, the second takes two
operations, the third takes three operations, etc. Therefore, the
total number of operations to
. You may object that the list is
not n long until all n items have been enqueued. Look at it this
way; the first item takes one operation, the second takes two
operations, the third takes three operations, etc. Therefore, the
total number of operations to enqueue n items is

We can express this as
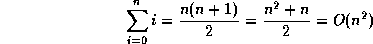
The implementation that provides  performance for each
performance for each
enqueue operation allows n items to be enqueued in
 time. This is significantly better than
time. This is significantly better than  (check the
chart for n = 100, for instance).
(check the
chart for n = 100, for instance).
Suppose you have a choice of two approaches to writing a program.
Both approaches have the same asymptotic performance (for example,
both are  ). Why select one over the other, they're both
the same, right? They may not be the same. There is this small
matter of the constant of proportionality.
Suppose algorithms
). Why select one over the other, they're both
the same, right? They may not be the same. There is this small
matter of the constant of proportionality.
Suppose algorithms A and B have the same asymptotic
performance,  . Now suppose that
. Now suppose that A
does ten operations for each data item, but algorithm B only
does three. It is reasonable to expect B to be faster than
A even though both have the same asymptotic performance. The
reason is that asymptotic analysis ignores constants of
proportionality.
As a specific example, let's say that algorithm A is
{
set up the algorithm, taking 50 time units;
read in n elements into array A; /* 3 units per element */
for (i = 0; i < n; i++)
{
do operation1 on A[i]; /* takes 10 units */
do operation2 on A[i]; /* takes 5 units */
do operation3 on A[i]; /* takes 15 units */
}
}
Let's now say that algorithm B is
{
set up the algorithm, taking 200 time units;
read in n elements into array A; /* 3 units per element */
for (i = 0; i < n; i++)
{
do operation1 on A[i]; /* takes 10 units */
do operation2 on A[i]; /* takes 5 units */
}
}
Algorithm A sets up faster than B, but does more
operations on the data. The execution time of A
and B will be
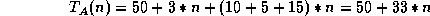
and
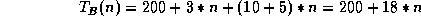
respectively.
The following graph shows the execution time for the two algorithms as
a function of n. Algorithm A is the better choice for small
values of n. For values of n > 10, algorithm B is the
better choice. Remember that both algorithms have time complexity
 .
.

Thomas A. Anastasio
Thu Nov 13 19:26:11 EST 1997
 if and only if there are constants
if and only if there are constants
 and
and  such that
such that  for all
for all  .
The expression
.
The expression  is read as ``T of n is in BigOh of f of n.''
BigOh is sometimes said to describe an ``upper-bound'' on the
complexity. Other forms of asymptotic analysis (``BigOmega'',
``LittleOh'', ``BigTheta'') are similar in spirit to BigOh, but will
not be discussed in this handout.
is read as ``T of n is in BigOh of f of n.''
BigOh is sometimes said to describe an ``upper-bound'' on the
complexity. Other forms of asymptotic analysis (``BigOmega'',
``LittleOh'', ``BigTheta'') are similar in spirit to BigOh, but will
not be discussed in this handout.
 , then eventually the value
, then eventually the value  will
exceed the value of
will
exceed the value of  . ``Eventually'' means ``after n
exceeds some value.'' Does this really mean anything useful? We might
say (correctly) that
. ``Eventually'' means ``after n
exceeds some value.'' Does this really mean anything useful? We might
say (correctly) that  , but we don't get a lot of
information from that;
, but we don't get a lot of
information from that;  is simply too big. When we use BigOh
analysis, we implicitly agree that the function
is simply too big. When we use BigOh
analysis, we implicitly agree that the function  we choose is
the smallest one that still satisfies the definition. It is correct
and meaningful to say
we choose is
the smallest one that still satisfies the definition. It is correct
and meaningful to say  ; this tells us
something about the growth pattern of the function
; this tells us
something about the growth pattern of the function  , namely
that the
, namely
that the  term will dominate the growth as n increases.
The following functions are often encountered in computer science BigOh
analysis:
term will dominate the growth as n increases.
The following functions are often encountered in computer science BigOh
analysis:
 . This is called constant growth.
. This is called constant growth.  does not grow at all as a function of n, it is a constant. It is
pronounced ``BigOh of one.'' For example, array access has this
characteristic.
does not grow at all as a function of n, it is a constant. It is
pronounced ``BigOh of one.'' For example, array access has this
characteristic.  . This is called logarithmic growth.
. This is called logarithmic growth.  grows as the base 2 logarithm of n (actually, the base doesn't
matter, it's just traditional to use base-2 in computer science).
It is pronounced ``BigOh of log n.'' For example, binary search has
this characteristic.
grows as the base 2 logarithm of n (actually, the base doesn't
matter, it's just traditional to use base-2 in computer science).
It is pronounced ``BigOh of log n.'' For example, binary search has
this characteristic.
 . This is called linear growth.
. This is called linear growth.  grows
linearly with n. It is pronounced ``BigOh of n.'' For example,
looping over all the elements in a one-dimensional array would be an
grows
linearly with n. It is pronounced ``BigOh of n.'' For example,
looping over all the elements in a one-dimensional array would be an
 operation.
operation.
 . This is called ``n log n'' growth.
. This is called ``n log n'' growth.  grows as n times the base 2 logarithm of n. It is pronounced
``BigOh of n log n.'' For example, heapsort and mergesort have this
characteristic. In fact, no sorting algorithm that uses comparison
between elements can be faster than
grows as n times the base 2 logarithm of n. It is pronounced
``BigOh of n log n.'' For example, heapsort and mergesort have this
characteristic. In fact, no sorting algorithm that uses comparison
between elements can be faster than  .
.
 . This is called polynomial growth.
. This is called polynomial growth.  grows
as the k-th power of n. In computer science, k is rarely
greater than 3. For example, selection sort is an
grows
as the k-th power of n. In computer science, k is rarely
greater than 3. For example, selection sort is an  algorithm.
It is pronounced ``BigOh of n squared.''
algorithm.
It is pronounced ``BigOh of n squared.''
 . This is called exponential growth.
. This is called exponential growth.  grows exponentially. It is pronounced ``BigOh of 2 to the n.''
Exponential growth is the most-feared growth pattern in computer
science; algorithms that grow this way are basically useless for
anything but very small problems.
grows exponentially. It is pronounced ``BigOh of 2 to the n.''
Exponential growth is the most-feared growth pattern in computer
science; algorithms that grow this way are basically useless for
anything but very small problems.
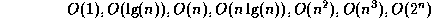
 then
then  . The ``='' sign does not mean equality in the usual
algebraic sense -- that's why it is pronounced ``
. The ``='' sign does not mean equality in the usual
algebraic sense -- that's why it is pronounced `` is in BigOh
of
is in BigOh
of  ,'' and not ``
,'' and not `` equals BigOh of
equals BigOh of  ,''
,''
 . To see this, let's assume that the setup
time is really long, say 500 time units. Let's also assume that the
time taken to read the data is 10 n, 10 time units for each data
point read. The following graph shows the function 500 + 10 n
plotted against n, the problem size. Also shown are the functions
n and 20 n.
. To see this, let's assume that the setup
time is really long, say 500 time units. Let's also assume that the
time taken to read the data is 10 n, 10 time units for each data
point read. The following graph shows the function 500 + 10 n
plotted against n, the problem size. Also shown are the functions
n and 20 n.

 and
and  such that
such that  when
when
 . One choice for these constants is
. One choice for these constants is  and
and  .
Therefore,
.
Therefore,  . (There are, of course, other choices
for
. (There are, of course, other choices
for  ; any value of
; any value of  will do.)
will do.)
 , n,
, n,  ,
,  ,
,  ,
and
,
and  to get some idea of their relative ``size.''
In the first graph, it looks like
to get some idea of their relative ``size.''
In the first graph, it looks like  and
and  are larger than
are larger than  . They're not; the second graph shows
the same data on an expanded scale. Clearly
. They're not; the second graph shows
the same data on an expanded scale. Clearly  when n > 4 and
when n > 4 and  when n > 10.
when n > 10.


 steps on a computer that does 1 billion steps/second.
steps on a computer that does 1 billion steps/second.
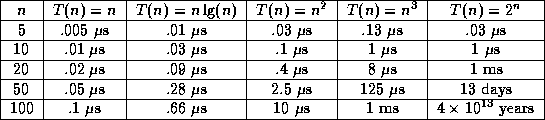
 , the compute time for
, the compute time for  has
started to become too large to be practical. This is most certainly
true when
has
started to become too large to be practical. This is most certainly
true when  . Even if we were to increase the speed of the
machine a million-fold,
. Even if we were to increase the speed of the
machine a million-fold,  for n = 100 would be 40,000,000 years,
a bit longer than you might want to wait for an answer.
for n = 100 would be 40,000,000 years,
a bit longer than you might want to wait for an answer.
 .
But, suppose we enqueue n items, one after another? The asymptotic
complexity will be
.
But, suppose we enqueue n items, one after another? The asymptotic
complexity will be  . You may object that the list is
not n long until all n items have been enqueued. Look at it this
way; the first item takes one operation, the second takes two
operations, the third takes three operations, etc. Therefore, the
total number of operations to
. You may object that the list is
not n long until all n items have been enqueued. Look at it this
way; the first item takes one operation, the second takes two
operations, the third takes three operations, etc. Therefore, the
total number of operations to 
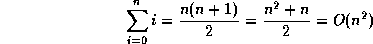
 performance for each
performance for each
 time. This is significantly better than
time. This is significantly better than  (check the
chart for n = 100, for instance).
(check the
chart for n = 100, for instance).
 ). Why select one over the other, they're both
the same, right? They may not be the same. There is this small
matter of the constant of proportionality.
Suppose algorithms
). Why select one over the other, they're both
the same, right? They may not be the same. There is this small
matter of the constant of proportionality.
Suppose algorithms  . Now suppose that
. Now suppose that 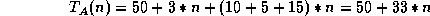
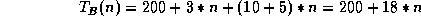
 .
.
