
CMSC--202 Computer Science II for Majors
Fall 1997 16 November 1997 Final Review
The final exam will be held at the following times and places. Please note that these are NOT the usual class times.

Every question from Exam 1 and from Exam 2 (the exams, not the reviews for the exams). The questions will be modified slightly so don't just memorize the answers.
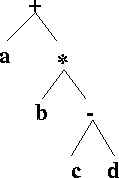
a*(b+c)-(d+(e-f)*g)
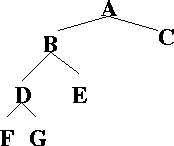
A?
E?
F?
B.
tree_type copy_tree(tree_type T)
that returns a copy of binary tree T
tree_type expand_leaf(tree_type T, tree_item_type x, tree_item_type y)that returns a new binary tree that is identical to the binary tree
T except that every leaf in T now has a left child and a
right child whose values are equal to x and y,
respectively. For example, invoking expand_leaf(T, 9, 12) on
the tree on the left produces the tree on the right.
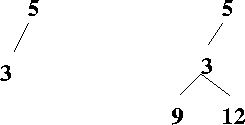
int height(tree_type T)
that returns the height of the binary tree T.
tree_type delete_root(tree_type T)that returns a new tree that contains every value stored in
T
except for the value stored in the root of T. The root of the
new tree should be one of the children of the root of T (the
other child must remain where it was); each child of the root of the
new tree should be either a child or a grandchild of the root of
T, and so on.
If delete_root is called on an empty tree, or
on a tree containing exactly one node, it should return
the_empty_tree. The function delete_root should be
non-destructive (not modify its argument in any way).
Hint: The base cases apply when T is empty or if the left child
is empty. If the left child is empty, the resultant tree is
the right child. Use wishful thinking
otherwise: ``if only I could delete the root of the
left child of T, then I could delete the root of T. I
would make the left child of T (with its root deleted) be the root
of the new tree. I
would use the right child of T as the right child of this new
root.''
BOOL same_tree(tree_type T1, tree_type T2)
that returns TRUE if binary trees T1 and T2 are exactly
the same (same values, same structure), and returns FALSE
otherwise. You may assume that values of tree_item_type can
be compared by means of the == operator.
tree_type bst_insert(tree_item_type item, tree_type T)that inserts item into the binary search tree T. After the insertion,
T must remain a binary search tree. You may assume
that tree_item_type values are comparable using the ==,
<, and > C operators.
Draw the binary search tree resulting from sequentially calling
bst_insert on an initially empty binary tree with the values
9,12,5,15,7,10,18.
void PreOrder(tree_type T, void (*operation)(tree_type))
that takes a binary tree T and performs operation on
each of its nodes during a preorder traversal.
char
void Foo(tree_type T)
that takes a binary tree, T, of char and performs some
function (your choice) on the tree. Briefly describe what the function
does in your own words.
PreOrder on the tree you
constructed above, using the function Foo you defined above.
Functions for DFS and BFS of binary trees from the notes will given to you in the exam, if needed.
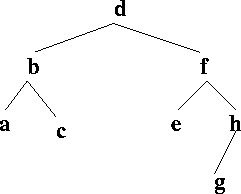
T be this tree
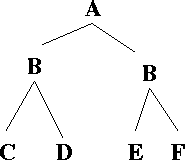
and let the function IsB be defined as
BOOL IsB(tree_type T)
{
return (tree_data(T) == 'B') ? TRUE : FALSE;
}
DFS(T, IsB)
BFS(T, IsB)
1,5,29,45,67,76,92,104,187,234 (in that order)
1, 5,29,45,67,76,92,104,187,234 (in that order)
29,234,1,45,92,76,67,187,104,5(in that order)
1,5,29,45,67,76,92,104,187,234 (in that order)
int hash(hash_item_type x)
{
return (x % 5);
}
qsort is
void qsort(void * base, size_t nmemb, size_t size,
int (* compar)(const void *, void *));
char * key, in addition to
at least one other field of your choice. The array should be assigned
to the variable A.
precedes as the compar function
for use with qsort on array A. precedes causes
sorting in ascending (lexicographic) order by the key field.
qsort that will sort A
N distinct items are there?
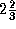 . Do this by using a comparison tree.
. Do this by using a comparison tree.
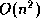 algorithm on average.
algorithm on average.
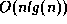 algorithm on average, but
is an
algorithm on average, but
is an 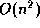 algorithm worst case.
algorithm worst case.
selectsort, mergesort,
and quicksort will be given to you on the exam if needed.
Given an array containing the integers 12 9 3 6 4 1 (in that
order),
selectsort. Show the array before the call to
the function swap. Show the array even if it is
unchanged.
mergesort Show the array before each call of the
function merge. Show the array even if it is unchanged.
quicksort Show the array before each call of the
function partition. Show the array even if it is unchanged.
from the set
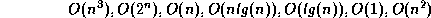
enqueue operations, is 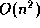 when the queue is
implemented as a simple list. What is the time complexity for the
pointer-based implementation of queue?
when the queue is
implemented as a simple list. What is the time complexity for the
pointer-based implementation of queue?