CMSC--202 Computer Science II for Majors
Fall 1997 22 October 1997 Exam 2 Review

Exam 2 will be a full-period exam. The exam will be taken entirely from the following questions, although some of the questions may be changed in minor ways.

Functional Parameters

All questions from the ``Functional Parameters'' handout.
Write the C function
```
   string find_sub(string, predicate)
```
that finds the first substring of a string which satisfies a given predicate. A string is a null-terminated char array. Write a typedef for the type predicate.
For example, if begins_with_vowel is a predicate that returns TRUE if its argument begins with a vowel ( i.e., one of the letters a, e, i, o, or u), and FALSE otherwise, then the call
```
   find_sub("grotesque", begins_with_vowel)
```
should return the substring "otesque". If no substring of the given string satisfies the predicate, find_sub should return NULL. For example, find_sub("pdq", begins_with_vowel) should return NULL.
Write a function
```
   int maximize(int (* f)(int), int low, int high)
```
that returns that integer value of the argument to f, between the bounds of low and high, inclusive which maximizes the value of the function f. For example,
```
  int foo(int x) { return (4-x) * (2 + x); }

  maximize(foo, -2, 2) ==> 1
```
because foo(1) = 9 (which is larger than the value that foo returns for any other integer between -2 and 2). Note that the return value is not 9.

Lists

For all questions in this section, you may use list_type, list_item_type, cons, first, rest, empty_list, and the_empty_list.

All exercises from 'Lists' handout.
Write a C function
```
  int count_pairs(list_type L, list_item_type item)
```
that returns the number of times that item appears twice in a row in L. For example, your function should exhibit the following behavior:
```
  count_pairs(<1 2 17 17 3>, 17)  ==> 1
  count_pairs(<1 17 2 17 3>, 17)  ==> 0
  count_pairs(<1 17 17 17 2>, 17) ==> 2
```
Notice that a given list element might take part in two pairs, as in the last example above.
Write a recursive C function
```
     BOOL is_member(list_item_type item, list_type L)
```
which returns TRUE if item is a member of L, and FALSE otherwise.
The counter function
```
   int counter(predicate p, list_type L)
```
returns the number of items on list L which satisfy predicate p. Write C code that uses counter to count the number of negative integers in a given list. Be sure to write the appropriate predicate and to show the call to counter. Do not write the code for counter.
The filter function
```
   list_type filter(predicate p, list_type L)
```
returns a list of the items on list L which satisfy predicate p. Write C code that uses filter to produce a list of the negative integers on a given list of integers. Be sure to write the appropriate predicate and to show the call to filter. Do not write the code for filter.
The transform function
```
  list_type transform(transformer f, list_type L)
```
returns a list composed of the values obtained by applying the transformer function f to the items on list L. Write C code that uses transform to produce a list of the squares of the integers on a given list. Be sure to write the appropriate transformer function and to show the call to transform. Do not write the code for transform.
Write C code, using filter and transform, that produces a list of those squares of the integers on a given list which are greater than 100 (the squares are greater than 100, not the integers on the list). Be sure to write the appropriate predicate and transformer.
Write a recursive C function
```
   list_type delete_first_n(list_type L, int n);
```
that returns a list composed of those items on list L after the nth. Assume that the first item on a list is number 1. In case n is greater than the length of list L, the_empty_list is to be returned. For example,
```
   delete_first_n(<1 2 3 4 5>, 2) ==> <3 4 5>
   delete_first_n(<1 2 3 4 5>, 5) ==> < >
   delete_first_n(<1 2 3 4 5>, 8) ==> < >
```
Write a recursive C function
```
   list_type delete_first_n_if(list_type L, predicate p, int n);
```
that returns a list composed of those items on list L which satisfy predicate p after the nth item on L. Assume that the first item on a list is number 1. In case n is greater than the length of list L, the_empty_list is to be returned. For example,
```
   delete_first_n_if(<1 2 3 4 5>, IsOdd, 2)  ==> <3 5>
   delete_first_n_if(<1 2 3 4 5>, IsEven, 2) ==> <4>
```
Write a recursive C function
```
   list_type delete_first(list_type L, int n)
```
that returns a list composed of the items on integer list L with the first occurrence of the integer n removed.
Write a recursive C function
```
   list_type merge(list_type L1, list_type L2)
```
that takes two sorted lists (increasing order) and returns the sorted list composed of the elements of lists L1 and L2. You may assume that all items on the lists are unique (no duplicate values). You may assume that the operators <, >, and == are valid of list_item_type data.
Write a recursive C function
```
    list_type InsertSorted(list_item_type item, list_type L)
```
which inserts item into the sorted list L such that L remains sorted. Duplicate items are allowed. You may assume that the operators <, >, and == are valid of list_item_type data.

Write a recursive C function

  list_type reduce_list(list_type L)

which returns a list composed of the sums of pairs of elements of integer list L. Examples:

  reduce_list(<1 2 3 4 5 6>) ==> <3 7 11>
  reduce_list(<1 2 3 4 5>)   ==> <3 7 5>
  reduce_list(<1 2 3 4>)     ==> <3 7>
  reduce_list(<1>)           ==> <1>
  reduce_list(<>)            ==> <>

Notice that if there is an odd number of items in L, the last value is copied unaltered to the result.

Write a recursive C function

  list_type max_truth(list_type L, predicate p)

that returns a list containing the largest element on list L that satisfies predicate p. If no element of L satisfies p, the empty list is returned. Examples:

  max_truth(<1 2 3 4 5>, is_odd) ==> <5>
  max_truth(<2 4 6 8>, is_odd)   ==> <>
  max_truth(<>, is_odd)          ==> <>
  max_truth(<2 4 5 3 6>, is_odd) ==> <5>
  max_truth(<-4 -7 -9>, is_odd)  ==> <-7>

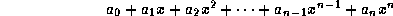
A polynomial in x is represented in mathematics in the form
The 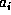terms are called coefficients. One or more of the coefficients may be zero. A polynomial can be represented in C as a list of coefficients in ascending order of exponent. For example, the polynomial
would be represented by the list <7 2 9 5> For the following questions, assume you have such a C representation, that it is typedef'd to poly and that all the primitive list operations work.
1. Write a recursive C function
```
    int MaxExpon(poly P)
```
  which returns the maximum exponent (not the maximum coefficient) in the polynomial P.
2. Write a recursive C function
```
   int EvaluatePoly(poly P, int x)
```
  which returns the value of the polynomial P when the polynomial variable has the value x. For example, for the polynomial represented mathematically as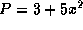
```
   EvaluatePoly(P, 2)  ==> 3 + 5*4  ==>  23
```
3. Write a recursive C function
```
    poly InsertTerm(int coeff, int expon, poly P)
```
  which returns a new polynomial that is P with coeff inserted in the proper expon position. Missing coefficients for exponents less than expon are inserted as zero. Examples:
```
   InsertTerm(5, 3, <2 7 4>)    ==>  <2 7 4 5>
   InsertTerm(5, 3, <2 7>)      ==>  <2 7 0 5>
   InsertTerm(5, 3, <2 7 4 6>   ==>  <2 7 4 5>
```
4. Write a recursive C function
```
   poly DeleteTerm(int expon, poly P)
```
  which returns a new polynomial that has all the terms of P except the term at exponent expon. The new polynomial is a simple copy of P if there is no such term. Examples:
```
   DeleteTerm(2, <2 7 4 6>)    ==>  <2 7 0 6>
   DeleteTerm(3, <2 7 4 6>)    ==>  <2 7 4>
   DeleteTerm(4, <2 7 4 6>)    ==>  <2 7 4 6>
```

Abstract Data Types

Each of the following questions means ``write an ADT, in English.'' To write an ADT, you describe two things, the elements of the ADT and the operations which may be performed on the elements. Do not write code! Do not say a word about implementation -- no implementation details! Remember, no implementation is to be discussed. In other words, there are no implementations associated with any ADT.

Write an ADT for lists of strings.
Write an ADT for stack.
Write an ADT for queue.

Stacks and Queues

In the questions in this section, unless otherwise indicated, assume that stack_item_type and queue_item_type are both int. Assume the stack and queue ADTs given in class. Stacks have create_stack, push, pop, empty_stack, and full_stack operations defined. Queues have create_queue, enqueue, dequeue, empty_queue, and full_queue operations defined.

All exercises from Stacks/Queues handout.

What is printed by the following code fragment?

  stack_type S = create_stack();
  queue_type Q = create_queue();
  int i;

  for (i = 2;  i < 6;  i++)
   {
     enqueue(i, Q);
     push(i, S);
   }

  for (i = 2; i < 5; i++)
    enqueue(dequeue(Q), Q);

  while (empty_stack(S) == FALSE)
    printf("%d ", (pop(S) == dequeue(Q)) );

A programmer wishes to do parenthesis matching, but does not want to use a stack. The programmer thus decides to simply keep three variables, ParenCount, BracketCount, and BraceCount to keep track of the number of '(', '[', and '{' characters, respectively. The idea is that when a left-paren is seen, the corresponding variable is incremented and when a right-paren is seen, the corresponding variable is decremented. The expression is said to have balanced parentheses if the three variables are all zero after the expression has been entirely read. Will this algorithm work for checking parenthesis-matching? If so, why? If not, say why not and give a counterexample.
Let Q be a non-empty queue and let S be an empty stack. Write C code to reverse the order of the items in Q.
Write a C function
```
   queue_type copy_queue(queue_type Q)
```
that returns a new queue containing all of the items in Q in the same order that they were found in Q. The original queue Q must end up unchanged.
Write a C function
```
     void SelectItem(stack_type S, stack_item_type n)
```
that finds the first occurrence of item n on stack S and moves it to the top of the stack, leaving the other stack items in their original order. You may assume that the operator == is valid for this stack_item_type. Note that the stack may be empty or that n may not be on the stack.
Write a C function
```
   void remove_if(stack_type S, predicate p)
```
that removes all elements of S that satisfy predicate p. Items on S that do not satisfy the predicate must remain on the stack in their original order.
Let S be a stack of positive integers and let x be an integer variable. Write C code fragments to perform each of the following operations:
1. Set x to the top element of S and leave the top element of S unchanged. If S is empty, set x to -1.
2. Set x to the third element from the top in S, provided that S contains at least three integers. If not, set x to -1. Leave S unchanged.
3. Set x to the bottom element of S (or to -1 if S is empty) and leave S unchanged.
4. Delete all occurrences of x from S, leaving the other elements of S in the same order.

Thomas A. Anastasio
Wed Oct 22 22:29:26 EDT 1997